
Peridynamics
Encyclopedia

Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
that is oriented toward deformations with discontinuities, especially fracture
Fracture
A fracture is the separation of an object or material into two, or more, pieces under the action of stress.The word fracture is often applied to bones of living creatures , or to crystals or crystalline materials, such as gemstones or metal...
s.
Purpose of peridynamics
The peridynamic theory is based on integral equationIntegral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s, in contrast with the classical theory of continuum mechanics, which is based on partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. Since partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s do not exist on crack surfaces and other singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
, the classical equations of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
cannot be applied directly when such features are present in a deformation. The integral equations of the peridynamic theory can be applied directly, because they do not require partial derivatives.
The ability to apply the same equations directly at all points in a mathematical model of a deforming structure helps the peridynamic approach avoid the need for the special techniques of fracture mechanics
Fracture mechanics
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
. For example, in peridynamics, there is no need for a separate crack growth law based on a stress intensity factor
Stress Intensity Factor
The stress intensity factor, K, is used in fracture mechanics to predict the stress state near the tip of a crack caused by a remote load or residual stresses. It is a theoretical construct usually applied to a homogeneous, linear elastic material and is useful for providing a failure criterion...
.
Definition and basic terminology
The basic equation of peridynamics is the following equation of motionEquation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
:

where
 is a point in a body
is a point in a body  ,
,  is time,
is time,  is the displacement vector
is the displacement vectorDisplacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
field, and
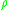 is the mass density in the undeformed body.
is the mass density in the undeformed body.x' is a dummy variable of integration.
The vector valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
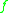 is the force density that
is the force density that  exerts on
exerts on  . This force density depends on the relative displacement and relative position vectors between
. This force density depends on the relative displacement and relative position vectors between  and
and  . The dimension
. The dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s of
 are force per volume squared. The function
are force per volume squared. The function 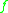 is called the "pairwise force function" and contains all the constitutive
is called the "pairwise force function" and contains all the constitutiveConstitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
(material-dependent) properties. It describes how the internal forces depend on the deformation.
The interaction between any
 and
and  is called a "bond." The physical mechanism in this interaction need not be specified.
is called a "bond." The physical mechanism in this interaction need not be specified.It is usually assumed that
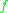 vanishes whenever
vanishes whenever 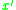 is outside a neighborhood of
is outside a neighborhood of  (in the undeformed configuration) called the horizon.
(in the undeformed configuration) called the horizon.
The term "peridynamic," an adjective, was proposed in the year 2000 and comes from the prefix peri, which means all around, near, or surrounding; and the root dyna, which means force or power. The term "peridynamics," a noun, is a shortened form of the phrase peridynamic model of solid mechanics.
Pairwise force functions
Using the abbreviated notation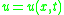 and
and 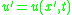
Newton's third law places the following restriction on
 :
:
for any
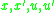 . This equation states that
. This equation states thatthe force density vector that
 exerts on
exerts on  equals minus the force density vector that
equals minus the force density vector that  exerts on
exerts on  . Balance of angular momentum
. Balance of angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
requires that
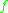 be parallel to the vector connecting the deformed position of
be parallel to the vector connecting the deformed position of  to the deformed position of
to the deformed position of 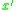 :
: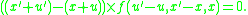
A pairwise force function is specified by a graph of
 versus bond elongation
versus bond elongation  , defined by
, defined by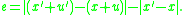
A schematic of a pairwise force function for the bond connecting two typical points is shown in the following figure:

Damage
Damage is incorporated in the pairwise force function by allowing bonds to break when their elongation exceeds some prescribed value. After a bond breaks, it no longer sustains any force, and the endpoints are effectively disconnected from each other. When a bond breaks, the force it was carrying is redistributed to other bonds that have not yet broken. This increased load makes it more likely that these other bonds will break. The process of bond breakage and load redistribution, leading to further breakage, is how cracks grow in the peridynamic model.Peridynamic states

To address this lack of generality, the idea of "peridynamic states" was introduced. This allows the force density in each bond to depend on the stretches in all the bonds connected to its endpoints, in addition to its own stretch. For example, the force in a bond could depend on the net volume changes at the endpoints. The effect of this volume change, relative to the effect of the bond stretch, determines the Poisson ratio. With peridynamic states, any material that can be modeled within the standard theory of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
can be modeled as a peridynamic material, while retaining the advantages of the peridynamic theory for fracture.
Further reading
- S. A. Silling, M. Zimmermann, and R. Abeyaratne, "Deformation of a Peridynamic Bar," Journal of Elasticity, Vol. 73 (2003) 173-190. DOI: 10.1023/B:ELAS.0000029931.03844.4f
- S. A. Silling and F. Bobaru, "Peridynamic Modeling of Membranes and Fibers," International Journal of Non-Linear Mechanics, Vol. 40 (2005) 395-409. DOI:10.1016/j.ijnonlinmec.2004.08.004
- O. Weckner and R. Abeyaratne, "The Effect of Long-Range Forces on the Dynamics of a Bar," Journal of the Mechanics and Physics of Solids, Vol. 53 (2005) 705-728. DOI: 10.1016/j.jmps.2004.08.006
- S. A. Silling and E. Askari, "A Meshfree Method Based on the Peridynamic Model of Solid Mechanics," Computers and Structures, Vol. 83 (2005) 1526-1535. DOI:10.1016/j.compstruc.2004.11.026
- K. Dayal and K. Bhattacharya, "Kinetics of Phase Transformations in the Peridynamic Formulation of Continuum Mechanics," Journal of the Mechanics and Physics of Solids, Vol. 54 (2006) 1811-1842.DOI: I0.1016/j.jmps.2006.04.001
- W. Gerstle, N. Sau, and S. Silling, "Peridynamic Modeling of Concrete Structures," Nuclear Engineering and Design, Vol. 237 (2007) 1250-1258. DOI: 10.1016/j.nucengdes.2006.10.002
- E. Emmrich and O. Weckner, "On the well-posedness of the linear peridynamic model and its convergence towards the Navier equation of linear elasticity," Communications in Mathematical Sciences, Vol. 5 (2007), pp. 851-864. http://www.intlpress.com/CMS/p/2007/issue5-4/CMS-5-4-A6-Emmrich.pdf
- S. A. Silling, M. Epton, O. Weckner, J. Xu and E. Askari, "Peridynamic States and Constitutive Modeling," Journal of Elasticity, Vol. 88 (2007) 151-184. DOI: 10.1007/s10659-007-9125-1
- F. Bobaru, "Influence of van der Waals forces on increasing the strength and toughness in dynamic fracture of nanofibre networks: a peridynamic approach," Modelling and Simulation in Materials Science and Engineering, Vol. 15 (2007) 397-417. DOI: 10.1088/0965-0393/15/5/002
- R. W. Macek and S. A. Silling, "Peridynamics via finite element analysis," Finite Elements in Analysis and Design, Vol. 43, Issue 15, (2007) 1169-1178. DOI: 10.1016/j.finel.2007.08.012
- S. A. Silling and R. B. Lehoucq, "Convergence of Peridynamics to Classical Elasticity Theory," Journal of Elasticity, Vol. 93 (2008) 13-37. DOI:10.1007/s10659-008-9163-3
- M. L. Parks, R. B. Lehoucq, S. Plimpton, and S. Silling, "Implementing peridynamics within a molecular dynamics code," Computer Physics Communications, Vol. 179 (2008), pp. 777-783. DOI:10.1016/j.cpc.2008.06.011
- F. Bobaru, M. Yang, L. F. Alves, S. A. Silling, E. Askari, and J. Xu, "Convergence, adaptive refinement, and scaling in 1D peridynamics," International Journal for Numerical Methods in Engineering, Vol. 77, Issue 6 (2009) 852-877. DOI: 10.1002/nme.2439
- E. Askari, F. Bobaru, R. B. Lehoucq, M. L. Parks, S. A. Silling, and O. Weckner, "Peridynamics for multiscale materials modeling," Scidac 2008. Journal of Physics: Conference Series, Vol. 125 (2008) 012078 (11pp). DOI: 10.1088/1742-6596/125/1/012078
- S. A. Silling, O. Weckner, E. Askari, and F. Bobaru, "Crack nucleation in a peridynamic solid," International Journal of Fracture, Vol. 162(1-2), (2010) 219-227. DOI: 10.1007/s10704-010-9447-z
- YD. Ha and F. Bobaru, "Studies of dynamic crack propagation and crack branching with peridynamics," International Journal of Fracture, Vol. 162(1-2), (2010) 229-244. doi:10.1007/s10704-010-9442-4
- F. Bobaru and M. Duangpanya, "The peridynamic formulation for transient heat conduction," International Journal of Heat and Mass Transfer, Vol. 53(19-20), (2010) 4047-4059. doi:10.1016/j.ijheatmasstransfer.2010.05.024
- S.A. Silling and R.B. Lehoucq,"Peridynamic Theory of Solid Mechanics," Advances in Applied Mechanics, Vol. 44, (2010) 73-168. DOI:10.1016/S0065-2156(10)44002-8
- YD. Ha and F. Bobaru, "Characteristics of dynamic brittle fracture captured with peridynamics," Engineering Fracture Mechanics, Vol. 78, (2011) 1156–1168. doi:10.1016/j.engfracmech.2010.11.020

