
Constitutive equation
Encyclopedia
In physics
, a constitutive equation is a relation between two physical quantities (especially kinetic quantities are related to kinematic quantities) that is specific to a material or substance, and approximates the response of that material to external forces. It is combined with other equations governing physical laws to solve physical problems, like the flow of a fluid in a pipe, or the response of a crystal to an electric field.
As an example, in structural analysis
, constitutive relations connect applied stresses
or force
s to strain
s or deformations. The stress-strain constitutive relation for linear materials commonly is known as Hooke's law
.
Some constitutive equations are simply phenomenological
; others are derived from first principles. A common approximate constitutive equation frequently is expressed as a simple proportionality using a parameter taken to be a property of the material, such as electrical conductivity or a spring constant. However, much more elaborate constitutive equations often are necessary to account for tensor
properties, the rate of response of materials and their non-linear behavior. See the article Linear response function
.
The first constitutive equation (constitutive law) was developed by Robert Hooke
and is known as Hooke's law. It deals with the case of linear elastic materials. Following this discovery, this type of equation, often called a "stress-strain relation" in this example, but also called a "constitutive assumption" or an "equation of state" was commonly used. Walter Noll
advanced the use of constitutive equations, clarifying their classification and the role of invariance requirements, constraints, and definitions of terms
like "material", "isotropic", "aeolotropic", etc. The class of "constitutive relations" of the form stress rate = f (velocity gradient, stress, density) was the subject of Walter Noll
's dissertation in 1954 under Clifford Truesdell
.
In modern condensed matter physics
, the constitutive equation plays a major role. See Linear constitutive equations and Nonlinear correlation functions.
Following are numerous examples of constitutive equations, many in frequent use.
and quantum physics, the precise dynamics of a system form a set of coupled
differential equation
s, which are almost always too complicated to be solved exactly, even at the level of statistical mechanics
. In the context of electromagnetism, this remark applies to not only the dynamics of free charges and currents (which enter Maxwell's equations directly), but also the dynamics of bound charges and currents (which enter Maxwell's equations through the constitutive relations). As a result, various approximation schemes are typically used.
For example, in real materials, complex transport equations must be solved to determine the time and spatial response of charges, for example, the Boltzmann equation
or the Fokker–Planck equation or the Navier-Stokes equations
. For example, see magnetohydrodynamics
, fluid dynamics
, electrohydrodynamics
, superconductivity
, plasma modeling
. An entire physical apparatus for dealing with these matters has developed. See for example, linear response theory
, Green–Kubo relations and Green's function (many-body theory)
.
These complex theories provide detailed formulas for the constitutive relations describing the electrical response of various materials, such as permittivities
, permeabilities
, conductivities and so forth.
- a field of solid state physics
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a constitutive equation is a relation between two physical quantities (especially kinetic quantities are related to kinematic quantities) that is specific to a material or substance, and approximates the response of that material to external forces. It is combined with other equations governing physical laws to solve physical problems, like the flow of a fluid in a pipe, or the response of a crystal to an electric field.
As an example, in structural analysis
Structural analysis
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
, constitutive relations connect applied stresses
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
or force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s to strain
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
s or deformations. The stress-strain constitutive relation for linear materials commonly is known as Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
.
Some constitutive equations are simply phenomenological
Phenomenology (science)
The term phenomenology in science is used to describe a body of knowledge that relates empirical observations of phenomena to each other, in a way that is consistent with fundamental theory, but is not directly derived from theory. For example, we find the following definition in the Concise...
; others are derived from first principles. A common approximate constitutive equation frequently is expressed as a simple proportionality using a parameter taken to be a property of the material, such as electrical conductivity or a spring constant. However, much more elaborate constitutive equations often are necessary to account for tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
properties, the rate of response of materials and their non-linear behavior. See the article Linear response function
Linear response function
A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response...
.
The first constitutive equation (constitutive law) was developed by Robert Hooke
Robert Hooke
Robert Hooke FRS was an English natural philosopher, architect and polymath.His adult life comprised three distinct periods: as a scientific inquirer lacking money; achieving great wealth and standing through his reputation for hard work and scrupulous honesty following the great fire of 1666, but...
and is known as Hooke's law. It deals with the case of linear elastic materials. Following this discovery, this type of equation, often called a "stress-strain relation" in this example, but also called a "constitutive assumption" or an "equation of state" was commonly used. Walter Noll
Walter Noll
Walter Noll is a mathematician, and Professor Emeritus at Carnegie Mellon University. He is best known for developing mathematical tools of classical mechanics and thermodynamics....
advanced the use of constitutive equations, clarifying their classification and the role of invariance requirements, constraints, and definitions of terms
like "material", "isotropic", "aeolotropic", etc. The class of "constitutive relations" of the form stress rate = f (velocity gradient, stress, density) was the subject of Walter Noll
Walter Noll
Walter Noll is a mathematician, and Professor Emeritus at Carnegie Mellon University. He is best known for developing mathematical tools of classical mechanics and thermodynamics....
's dissertation in 1954 under Clifford Truesdell
Clifford Truesdell
Clifford Ambrose Truesdell III was an American mathematician, natural philosopher, historian of science, and polemicist.-Life:...
.
In modern condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, the constitutive equation plays a major role. See Linear constitutive equations and Nonlinear correlation functions.
Following are numerous examples of constitutive equations, many in frequent use.
Definitions
| Nomenclature |
|---|
| F = friction Friction Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:... force (N) R = reaction force Reaction (physics) The third of Newton's laws of motion of classical mechanics states that forces always occur in pairs. Every action is accompanied by a reaction of equal magnitude but opposite direction. This principle is commonly known in the Latin language as actio et reactio. The attribution of which of the two... at point of contact (N) |
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Static, kinetic, and rolling friction Friction Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:... coefficients |
μ, μf | 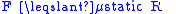   Normal force to a surface: 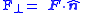 |
dimensionless | dimensionless |
Definitive laws
| Property/effect | Equation |
|---|---|
| Hooke's law Hooke's law In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law... , defines elasticity/spring constants |
Scalar forms: 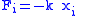 or  Tensor forms, 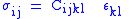 or inversely, 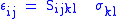 |
| F = tensile/compressive force (N) x = extended/contracted displacement Displacement (vector) A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P... (m) σ = stress (Pa) ε = strain Deformation (mechanics) Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body... (dimensionless) k = (Hooke's Law) spring constant (N m−1) Y = Young's modulus Young's modulus Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain... (Pa) C = elasticity tensor Hooke's law In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law... (Pa) S = compliance tensor Hooke's law In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law... (dimensionless) |
|
| Newton's law of experimental impact, defines coefficient of restitution Coefficient of restitution The coefficient of restitution of two colliding objects is a fractional value representing the ratio of speeds after and before an impact, taken along the line of the impact... |
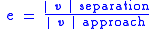 Usually 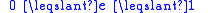 , , but it is possible that 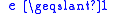 |
| e = Coefficient of restitution Coefficient of restitution The coefficient of restitution of two colliding objects is a fractional value representing the ratio of speeds after and before an impact, taken along the line of the impact... vseparation = relative velocity of separation (m s−1) vapproach = relative velocity of approach (m s−1) |
|
Transport phenomena
| Nomenclature |
|---|
| x = displacement of substance(m) A = Cross-section Area Cross section (geometry) In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc... (m2) v = Flow velocity Flow velocity In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid... (m s−1) μ = Fluid viscosity Viscosity Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity... (Pa s) Fd = Drag force Drag (physics) In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity... (N) g = Standard gravitational acceleration = 9.81 N kg-1 ρ = Volume mass density of fluid (kg m−3) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Drag equation Drag equation In fluid dynamics, the drag equation is a practical formula used to calculate the force of drag experienced by an object due to movement through a fully enclosing fluid.... , drag coefficient Drag coefficient In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or... |
cd | 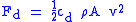 |
dimensionless | dimensionless |
Definitive laws
| Property/effect | Equation |
|---|---|
| Fick's law of diffusion Diffusion Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles... , defines diffusion coefficient D |
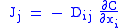 |
| D = mass diffusion coefficient (m2 s−1) J = diffusion flux of substance (mol m−2 s−1) ∂C/∂x = (1d)concentration Concentration In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration... gradient of substance (mol dm−4) |
|
| Darcy's law Darcy's law Darcy's law is a phenomenologically derived constitutive equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on the results of experiments on the flow of water through beds of sand... for porous flow in matter, defines permeability κ |
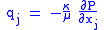 |
| κ = permeability of medium (m2) q = discharge flux of substance (m s−1) ∂P/∂x = (1d) pressure gradient Pressure gradient In atmospheric sciences , the pressure gradient is a physical quantity that describes in which direction and at what rate the pressure changes the most rapidly around a particular location. The pressure gradient is a dimensional quantity expressed in units of pressure per unit length... of system (Pa m−1) |
|
Equations
| Property/effect | Equation |
|---|---|
| Terminal velocity Terminal velocity In fluid dynamics an object is moving at its terminal velocity if its speed is constant due to the restraining force exerted by the fluid through which it is moving.... |
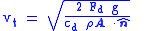 |
| vt = terminal velocity within fluid (m s-1) |
|
| Newtonian fluid Newtonian fluid A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:... |
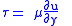 |
| τ = shear stress exerted by fluid (Pa) ∂u/∂y = velocity gradient perp. to shear direction, strain rate (s−1) |
|
Thermodynamics
| Nomenclature |
|---|
| L = length of material (m) Δx = Displacement of heat transfer (m) A = surface cross section (m2) V = Volume (m3) T = Temperature (K) ∇T = temperature gradient (K m−1) q = heat energy (J) P = thermal current, thermal power (W) ε = strain or emmisivity (both dimensionless) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| General heat capacity Heat capacity Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount... |
C = Heat capacity |  |
J K−1 | |
| Linear thermal expansion Thermal expansion Thermal expansion is the tendency of matter to change in volume in response to a change in temperature.When a substance is heated, its particles begin moving more and thus usually maintain a greater average separation. Materials which contract with increasing temperature are rare; this effect is... |
α = Linear coefficient of linear thermal expansion | 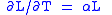 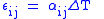 |
K−1 | [Θ]−1 |
| Volumetric thermal expansion | β, γ |  |
K−1 | |
| Thermal conductivity | κ, K, λ | 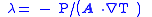 |
W m−1 K−1 | |
| Thermal conductance | U | 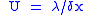 |
W m−2 K−1 | |
| Thermal resistance | R | 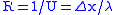 |
m2 K W−1 | |
Definitive laws
| Property/effect | Equation |
|---|---|
| Fourier's law of thermal conduction, defines thermal conductivity Thermal conductivity In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction.... λ |
 |
| λ = Thermal conductivity Thermal conductivity In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction.... (W m−1 K−1 ) q = heat flux (W m−2) ∂T/∂x = (1d) Temperature gradient Temperature gradient A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature gradient is a dimensional quantity expressed in units of degrees per unit length... (K m−1) |
|
| Stefan–Boltzmann law of black-body radiation, defines emmisivity ε | For a single radiator: For a temperature differance: 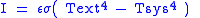 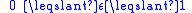 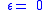 for perfect reflector for perfect reflector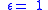 for perfect absorber (true black body) for perfect absorber (true black body) |
| I = radiant intensity Radiant intensity In radiometry, radiant intensity is a measure of the intensity of electromagnetic radiation. It is defined as power per unit solid angle. The SI unit of radiant intensity is watts per steradian . Radiant intensity is distinct from irradiance and radiant exitance, which are often called intensity... (W m−2) σ = Stefan–Boltzmann constant (W m−2 K−4) Tsys = temperature of radiating system(K) Text = temperature of external surroundings (K) T = temperature (K) ε = emissivity Emissivity The emissivity of a material is the relative ability of its surface to emit energy by radiation. It is the ratio of energy radiated by a particular material to energy radiated by a black body at the same temperature... (dimensionless) |
|
| Ideal gas law Ideal gas law The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law... , defines parameters of an ideal gas |
 |
| p = pressure (Pa) T = temperature Temperature Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot... (K) V = volume (m−3) R = gas constant Gas constant The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,... (J K−1 mol−1) n = number of moles, amount of substance Amount of substance Amount of substance is a standards-defined quantity that measures the size of an ensemble of elementary entities, such as atoms, molecules, electrons, and other particles. It is sometimes referred to as chemical amount. The International System of Units defines the amount of substance to be... (mol) |
|
Constitutive equations in electromagnetism and related areas
In both classicalClassical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
and quantum physics, the precise dynamics of a system form a set of coupled
Simultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, which are almost always too complicated to be solved exactly, even at the level of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. In the context of electromagnetism, this remark applies to not only the dynamics of free charges and currents (which enter Maxwell's equations directly), but also the dynamics of bound charges and currents (which enter Maxwell's equations through the constitutive relations). As a result, various approximation schemes are typically used.
For example, in real materials, complex transport equations must be solved to determine the time and spatial response of charges, for example, the Boltzmann equation
Boltzmann equation
The Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of one particle in rarefied gas...
or the Fokker–Planck equation or the Navier-Stokes equations
Navier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
. For example, see magnetohydrodynamics
Magnetohydrodynamics
Magnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...
, fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, electrohydrodynamics
Electrohydrodynamics
Electrohydrodynamics , also known as electro-fluid-dynamics or electrokinetics, is the study of the dynamics of electrically charged fluids. It is the study of the motions of ionised particles or molecules and their interactions with electric fields and the surrounding fluid...
, superconductivity
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
, plasma modeling
Plasma modeling
Plasma Modeling refers to solving equations of motion that describe the state of a plasma. It is generally coupled with Maxwell's Equations for electromagnetic fields...
. An entire physical apparatus for dealing with these matters has developed. See for example, linear response theory
Linear response function
A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response...
, Green–Kubo relations and Green's function (many-body theory)
Green's function (many-body theory)
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators....
.
These complex theories provide detailed formulas for the constitutive relations describing the electrical response of various materials, such as permittivities
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
, permeabilities
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
, conductivities and so forth.
| Nomenclature |
|---|
| E = electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... (N C−1) D = electric displacement field (Cm−2) P = polarization density Polarization density In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is... (C m−2) B = magnetic flux density, induction field (T = N A−1 m−1) H = magnetic field intensity Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... (A m−1) M = magnetization Magnetization In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material... field (A m−1) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Electrical resistance Electrical resistance The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical... |
R | 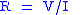 |
Ω = V A−1 = J s C−2 | [M] [L]2 [T]−3 [I]−2 |
| Resistivity Electrical resistivity and conductivity Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre... |
ρ | 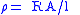 |
Ω m | [M]2 [L]2 [T]−3 [I]−2 |
| Resistivity temperature coefficient Temperature coefficient The temperature coefficient is the relative change of a physical property when the temperature is changed by 1 K.In the following formula, let R be the physical property to be measured and T be the temperature at which the property is measured. T0 is the reference temperature, and ΔT is the... , linear temperature dependence |
α | 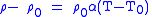 |
K−1 | [Θ]−1 |
| Electrical conductance | G | 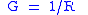 |
S = Ω−1 | [T]3 [I]2 [M]−1 [L]−2 |
| Electrical conductivity Electrical resistivity and conductivity Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre... |
σ | 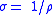 |
Ω−1 m−1 | [I]2 [T]3 [M]−2 [L]−2 |
| Relative permittivity (aka dielectric constant) | εr | can only be found from experiment | F m−1 | [I]2 [T]4 [M]−1 [L]−3 |
| (Absolute) dielectric permittivity Permittivity In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how... |
ε | 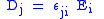 |
F m−1 | [I]2 [T]4 [M]−1 [L]−3 |
| Electric susceptibility Electric susceptibility In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field... |
χE | 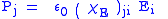 |
dimensionless | dimensionless |
| Magnetic reluctance Magnetic reluctance Magnetic reluctance, or magnetic resistance, is a concept used in the analysis of magnetic circuits. It is analogous to resistance in an electrical circuit, but rather than dissipating magnetic energy it stores magnetic energy... |
R, Rm,  |
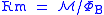 |
A Wb-1 = H-1 | [M]-1[L]-2[T]2 |
| Magnetic permeance | P, Pm, Λ,  |
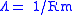 |
Wb A-1 = H | [M][L]2[T]-2 |
| Relative permeability | μr | can only be found from experiment | dimensionless | dimensionless |
| Absolute magnetic permeability Permeability (electromagnetism) In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically... |
μ | 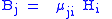 |
H m−1 | |
| Magnetic susceptibility Magnetic susceptibility In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field... |
χM | 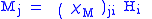 |
dimensionless | dimensionless |
Relations
| Property/effect | Equation |
|---|---|
| Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... vectors |
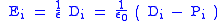 |
| Magnetic field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... Vectors |
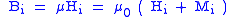 |
| Permittivity |  |
| Permeability |  |
Laws
| Property/effect | Equation |
|---|---|
| Ohm's law Ohm's law Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points... of electric conduction, defines electric conductivity (and so resistivity and resistance) |
Simplist form is: 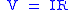 More general forms are: 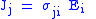 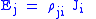 |
| J = Electric Current Density Electric current Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire... (A m−2) σ = Electric Conductivity Electrical resistivity and conductivity Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre... (Ω−1 m−1) ρ = Electrical resistivity (Ω m) |
|
Photonics
| Nomenclature |
|---|
| c = luminal speed in medium (m s−1) c0 = luminal speed in vacuum (m s−1) ε = electric permittivity of medium (F m−1) ε0 = vacuum electric permittivity (F m−1) εr = relative electric permittivity of medium (F m−1) μ = magnetic permeability of medium (H m−1) μ0 = vacuum magnetic permeability (H m−1) μr = relative magnetic permeability of medium (H m−1) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Refractive index Refractive index In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium.... |
n | 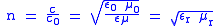 |
dimensionless | dimensionless |
Relations
| Property/effect | Equation |
|---|---|
| Luminal speed Speed of light The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time... in matter |
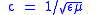 for special case of vacuum; ε = ε0 and μ = μ0, 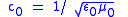 |
Solid state physics
These constitutive equations are often used in crystallographyCrystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
- a field of solid state physics
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
.
| Nomenclature |
|---|
| x = displacement (m) s = thickness of hall/probe (m) σ = mechanical stress (Pa) ε = mechanical strain (dimensionless) e = electron charge (C) n = charge carrier density Charge carrier density The charge carrier density denotes the number of charge carriers per volume. It is measured in m−3. As any density it can depend on position.It should not be confused with the charge density, which is the number of charges per volume at a given energy.... E = electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... (N C−1) D = electric displacement field (Cm−2) P = dielectric polarization density Polarization density In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is... (C m−2) B = magnetic flux density, induction field (T = N A−1 m−1) H = Magnetic Field Intensity Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... (A m−1) M = magnetization Magnetization In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material... field (A m−1) I = electric current (across Hall plate) (A) J = electric current density (A m−2) ρ = electrical resistivity (Ω m) a = dielectric impermeability (K) VH = Hall voltage (V) T = temperature (K) S = entropy (J K−1) q = heat flux (W m−2) |
Definitions
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Pyroelectricity Pyroelectricity Pyroelectricity is the ability of certain materials to generate a temporary voltage when they are heated or cooled. The change in temperature modifies the positions of the atoms slightly within the crystal structure, such that the polarization of the material changes. This polarization change... , pyroelectric coefficient |
p | 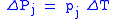 |
C m−2 K−1 | |
| Electrocaloric effect Electrocaloric effect The electrocaloric effect is phenomenon in which a material shows a reversible temperature change under an applied electric field. It is often considered to be the physical inverse of the pyroelectric effect.... , pyroelectric coefficient |
p | 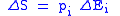 |
C m−2 K−1 | [I][T][L]-2[Θ]-1 |
| Seebeck effect, thermopower coefficient | β | 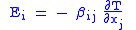 |
V K−1 | |
| Hall effect Hall effect The Hall effect is the production of a voltage difference across an electrical conductor, transverse to an electric current in the conductor and a magnetic field perpendicular to the current... , Hall coefficient |
RH |  |
C-1 | [I]-1[T]-1 |
| Peltier effect, peltier coefficient | Π | 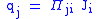 |
W A−1 | |
| Direct piezoelectric effect Piezoelectricity Piezoelectricity is the charge which accumulates in certain solid materials in response to applied mechanical stress. The word piezoelectricity means electricity resulting from pressure... , direct piezoelectric coefficient |
d, de | 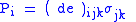 |
K−1 | |
| Converse piezoelectric effect Piezoelectricity Piezoelectricity is the charge which accumulates in certain solid materials in response to applied mechanical stress. The word piezoelectricity means electricity resulting from pressure... , direct piezoelectric coefficient |
d, de' | 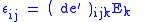 |
K−1 | |
| Piezomagnetic effect, piezomagnetic coefficient | q, dm | 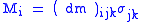 |
K−1 | |
| Piezooptic effect Piezooptic effect The piezooptic effect is manifest as a change in refractive index, n, of a material caused by a change in pressure on that material. Early demonstrations of the piezooptic effect were done on liquids. The effect has since been demonstrated in solid, crystalline materials.... , piezooptic coefficient |
Π | 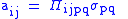 |
K−1 | |
Equations
| Property/effect | Equation |
|---|---|
| Hall effect Hall effect The Hall effect is the production of a voltage difference across an electrical conductor, transverse to an electric current in the conductor and a magnetic field perpendicular to the current... |
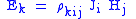 |

