
Mumford–Tate group
Encyclopedia
In algebraic geometry
, the Mumford–Tate group MT(F) constructed from a Hodge structure
F is a certain algebraic group
G, named for David Mumford
and John Tate
. When F is given by a rational representation
of an algebraic torus
, the definition of G is as the Zariski closure of the image in the representation of the circle group, over the rational numbers. It has been said that “Mumford–Tate groups have emerged as the principal symmetry groups in Hodge theory
”. They are applied to problems in number theory and physics, as well as geometry.
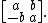
The circle group inside this group of matrices is the unitary group
U(1).
Hodge structures arising in geometry, for example on the cohomology groups of Kähler manifold
s, have a lattice consisting of the integral cohomology classes. Not quite so much is needed for the definition of the Mumford–Tate group, but it does assume that the vector space V underlying the Hodge structure has a given rational structure, i.e. is given over the rational numbers Q. For the purposes of the theory the complex vector space VC, obtained by extending the scalars of V from Q to C, is used.
The weight k of the Hodge structure describes the action of the diagonal matrices of T, and V is supposed therefore to be homogeneous of weight k, under that action. Under the action of the full group VC breaks up into subspaces Vpq, complex conjugate in pairs under switching p and q. Thinking of the matrix in terms of the complex number λ it represents, Vpq has the action of λ by the pth power and of the complex conjugate of λ by the qth power. Here necessarily
In more abstract terms, the torus T underlying the matrix group is the Weil restriction
of the multiplicative group
GL(1), from the complex field to the real field, an algebraic torus whose character group consists of the two homomorphisms to GL(1), interchanged by complex conjugation.
Once formulated in this fashion, the rational representation ρ of T on V setting up the Hodge structure F determines the image ρ(U(1)) in GL(VC); and MT(F) is by definition the Zariski closure, for the Q-Zariski topology on GL(V), of this image.
of an abelian variety
A. Conjecturally, the image of such a Galois representation, which is an l-adic Lie group for a given prime number l, is determined by the corresponding Mumford–Tate group G (coming from the Hodge structure on H1(A)), to the extent that knowledge of G determines the Lie algebra
of the Galois image. This conjecture is known only in particular cases. Through generalisations of this conjecture, the Mumford–Tate group has been connected to the motivic Galois group, and, for example, the general issue of extending the Sato–Tate conjecture (now a theorem).
, in the sense of the field generated by its entries, predicted by the dimension of its Mumford–Tate group, as in the previous section. Work of Pierre Deligne
has shown that the dimension bounds the transcendence degree; so that the Mumford–Tate group catches sufficiently many algebraic relations between the periods. This is a special case of the full Grothendieck period conjecture.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Mumford–Tate group MT(F) constructed from a Hodge structure
Hodge structure
In mathematics, a Hodge structure, named after W. V. D. Hodge, is an algebraic structure at the level of linear algebra, similar to the one that Hodge theory gives to the cohomology groups of a smooth and compact Kähler manifold...
F is a certain algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
G, named for David Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
and John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
. When F is given by a rational representation
Rational representation
In mathematics, in the representation theory of algebraic groups, a linear representation of an algebraic group is said to be rational if, viewed as a map from the group to the general linear group, it is a rational map of algebraic varieties....
of an algebraic torus
Algebraic torus
In mathematics, an algebraic torus is a type of commutative affine algebraic group. These groups were named by analogy with the theory of tori in Lie group theory...
, the definition of G is as the Zariski closure of the image in the representation of the circle group, over the rational numbers. It has been said that “Mumford–Tate groups have emerged as the principal symmetry groups in Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
”. They are applied to problems in number theory and physics, as well as geometry.
Formulation
The algebraic torus T used to describe Hodge structures has a concrete matrix representation, as the 2×2 invertible matrices of the shape that is given by the action of a+bi on the basis {1,i} of the complex numbers C over R: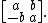
The circle group inside this group of matrices is the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(1).
Hodge structures arising in geometry, for example on the cohomology groups of Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s, have a lattice consisting of the integral cohomology classes. Not quite so much is needed for the definition of the Mumford–Tate group, but it does assume that the vector space V underlying the Hodge structure has a given rational structure, i.e. is given over the rational numbers Q. For the purposes of the theory the complex vector space VC, obtained by extending the scalars of V from Q to C, is used.
The weight k of the Hodge structure describes the action of the diagonal matrices of T, and V is supposed therefore to be homogeneous of weight k, under that action. Under the action of the full group VC breaks up into subspaces Vpq, complex conjugate in pairs under switching p and q. Thinking of the matrix in terms of the complex number λ it represents, Vpq has the action of λ by the pth power and of the complex conjugate of λ by the qth power. Here necessarily
- p + q = k.
In more abstract terms, the torus T underlying the matrix group is the Weil restriction
Weil restriction
In mathematics, restriction of scalars is a functor which, for any finite extension of fields L/k and any algebraic variety X over L, produces another variety ResL/kX, defined over k...
of the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
GL(1), from the complex field to the real field, an algebraic torus whose character group consists of the two homomorphisms to GL(1), interchanged by complex conjugation.
Once formulated in this fashion, the rational representation ρ of T on V setting up the Hodge structure F determines the image ρ(U(1)) in GL(VC); and MT(F) is by definition the Zariski closure, for the Q-Zariski topology on GL(V), of this image.
Mumford–Tate conjecture
The original context for the formulation of the group in question was the question of the Galois representation on the Tate moduleTate module
In mathematics, a Tate module of an abelian group, named for John Tate, is a module constructed from an abelian group A. Often, this construction is made in the following situation: G is a commutative group scheme over a field K, Ks is the separable closure of K, and A = G...
of an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
A. Conjecturally, the image of such a Galois representation, which is an l-adic Lie group for a given prime number l, is determined by the corresponding Mumford–Tate group G (coming from the Hodge structure on H1(A)), to the extent that knowledge of G determines the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of the Galois image. This conjecture is known only in particular cases. Through generalisations of this conjecture, the Mumford–Tate group has been connected to the motivic Galois group, and, for example, the general issue of extending the Sato–Tate conjecture (now a theorem).
Period conjecture
A related conjecture on abelian varieties states that the period matrix of A over number field has transcendence degreeTranscendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
, in the sense of the field generated by its entries, predicted by the dimension of its Mumford–Tate group, as in the previous section. Work of Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
has shown that the dimension bounds the transcendence degree; so that the Mumford–Tate group catches sufficiently many algebraic relations between the periods. This is a special case of the full Grothendieck period conjecture.
External links
- Lecture slides (PDF) by Phillip GriffithsPhillip GriffithsPhillip Griffiths is an American mathematician, known for his work in the field of geometry, and in particular for the complex manifold approach to algebraic geometry. He was a major developer in particular of the theory of variation of Hodge structure in Hodge theory and moduli theory.He received...
- Mumford-Tate groups, families of Calabi-Yau varieties and analogue André-Oort problems I, preprint (PDF)

