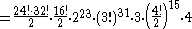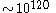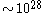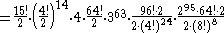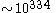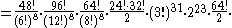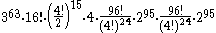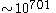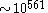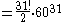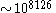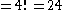N-dimensional sequential move puzzles

Rubik's Cube

Rubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...

is the original and best known of the three-dimensional sequential move puzzles. There have been many virtual implementations of this puzzle in software. It is a natural extension to create sequential move puzzles in more than three dimensions. Although no such puzzle could ever be physically constructed, the rules of how they operate are quite rigorously defined mathematically and are analogous to the rules found in three-dimensional geometry. Hence, they can be simulated by software. As with the mechanical sequential move puzzles, there are records for solvers, although not yet the same degree of competitive organisation.

Glossary

Vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

. A zero-dimensional point at which higher-dimension figures meet.
Edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....

. A one-dimensional figure at which higher-dimension figures meet.
Face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...

. A two-dimensional figure at which (for objects of dimension greater than three) higher-dimension figures meet.
Cell
Cell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...

. A three-dimensional figure at which (for objects of dimension greater than four) higher-dimension figures meet.
n-Polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

. A n-dimensional figure continuing as above. A specific geometric shape may replace polytope where this is appropriate, such as 4-cube to mean the tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

.

n-cell. A higher-dimension figure containing n cells.
Piece. A single moveable part of the puzzle having the same dimensionality as the whole puzzle.
Cubie. In the solving community this is the term generally used for a 'piece'.
Sticker. The coloured labels on the puzzle which identify the state of the puzzle. For instance, the corner cubies of a Rubik cube are a single piece but each has three stickers. The stickers in higher-dimensional puzzles will have a dimensionality greater than two. For instance, in the 4-cube, the stickers are three-dimensional solids.

For comparison purposes, the data relating to the standard 3³ Rubik cube is as follows;

Piece count
Number of vertices (V)	8	Number of 3-colour pieces	8
Number of edges (E)	12	Number of 2-colour pieces	12
Number of faces (F)	6	Number of 1-colour pieces	6
Number of cells (C)	1	Number of 0-colour pieces	1
Number of coloured pieces (P)	26
Number of stickers	54

Number of achievable combinations

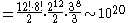
There is some debate over whether the face-centre cubies should be counted as separate pieces as they cannot be moved relative to each other. A different number of pieces may be given in different sources. In this article the face-centre cubies are counted as this makes the arithmetical sequences more consistent and they can certainly be rotated, a solution of which requires algorithms. However, the cubie right in the middle is not counted because it has no visible stickers and hence requires no solution. Arithmetically we should have

But P is always one short of this (or the n-dimensional extension of this formula) in the figures given in this article because C (or the corresponding highest-dimension polytope, for higher dimensions) is not being counted.

Magic 4D Cube

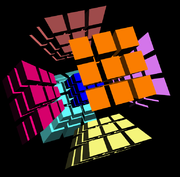
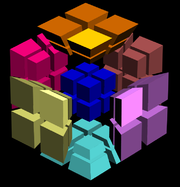
Geometric shape: tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

The Superliminal MagicCube4D software is capable of rendering 4-cube puzzles in four sizes, namely 2⁴, the standard 3⁴, 4⁴, and 5⁴. As well as the ability to make moves on the cube there are controls to change the view. These include controls for rotating the whole cube in 3-space and 4-space, 4-D perspective, cubie size and spacing, and sticker size.

Superliminal Software maintains a Hall of Fame for record breaking solvers of this puzzle.

3⁴ 4-cube

Piece count
Number of vertices	16	Number of 4-colour pieces	16
Number of edges	32	Number of 3-colour pieces	32
Number of faces	24	Number of 2-colour pieces	24
Number of cells	8	Number of 1-colour pieces	8
Number of 4-cubes	1	Number of 0-colour pieces	1
Number of coloured pieces	80
Number of stickers	216

Achievable combinations:

2⁴ 4-cube

Piece count
Number of vertices	16	Number of 4-colour pieces	16
Number of edges	32	Number of 3-colour pieces	0
Number of faces	24	Number of 2-colour pieces	0
Number of cells	8	Number of 1-colour pieces	0
Number of 4-cubes	1	Number of 0-colour pieces	0
Number of coloured pieces	16
Number of stickers	64

Achievable combinations:

4⁴ 4-cube

Piece count
Number of vertices	16	Number of 4-colour pieces	16
Number of edges	32	Number of 3-colour pieces	64
Number of faces	24	Number of 2-colour pieces	96
Number of cells	8	Number of 1-colour pieces	64
Number of 4-cubes	1	Number of 0-colour pieces	16
Number of coloured pieces	240
Number of stickers	512

Achievable combinations:

5⁴ 4-cube

Piece count
Number of vertices	16	Number of 4-colour pieces	16
Number of edges	32	Number of 3-colour pieces	96
Number of faces	24	Number of 2-colour pieces	216
Number of cells	8	Number of 1-colour pieces	216
Number of 4-cubes	1	Number of 0-colour pieces	81
Number of coloured pieces	544
Number of stickers	1000

Achievable combinations:

Magic 5D Cube

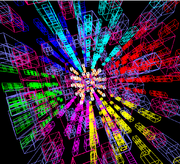
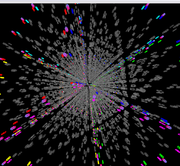
Geometric shape: penteract
Penteract
In five dimensional geometry, a 5-cube is a name for a five dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract hypercells....

The Gravitation3d Magic 5D Cube software is capable of rendering 5-cube puzzles in six sizes from 2⁵ to 7⁵. As well as the ability to make moves on the cube there are controls to change the view. These include controls for rotating the cube in 3-space, 4-space and 5-space, 4-D and 5-D perspective controls, cubie and sticker spacing and size controls, similar to Subliminal's 4D cube.

However, a 5-D puzzle is much more difficult to comprehend on a 2-D screen than a 4-D puzzle is. An essential feature of the Gravitation3d implementation is the ability to turn off or highlight chosen cubies and stickers. Even so, the complexities of the images produced are still quite severe as can be seen from the screen shots.

Gravitation3d maintains a Hall of Insanity for record breaking solvers of this puzzle. As of 6th, January 2011, there has been two successful solutions for the 7⁵ size of 5-cube.

3⁵ 5-cube

Piece count
Number of vertices	32	Number of 5-colour pieces	32
Number of edges	80	Number of 4-colour pieces	80
Number of faces	80	Number of 3-colour pieces	80
Number of cells	40	Number of 2-colour pieces	40
Number of 4-cubes	10	Number of 1-colour pieces	10
Number of 5-cubes	1	Number of 0-colour pieces	1
Number of coloured pieces	242
Number of stickers	810

Achievable combinations:

2⁵ 5-cube

Piece count
Number of vertices	32	Number of 5-colour pieces	32
Number of edges	80	Number of 4-colour pieces	0
Number of faces	80	Number of 3-colour pieces	0
Number of cells	40	Number of 2-colour pieces	0
Number of 4-cubes	10	Number of 1-colour pieces	0
Number of 5-cubes	1	Number of 0-colour pieces	0
Number of coloured pieces	32
Number of stickers	160

Achievable combinations:

4⁵ 5-cube

Piece count
Number of vertices	32	Number of 5-colour pieces	32
Number of edges	80	Number of 4-colour pieces	160
Number of faces	80	Number of 3-colour pieces	320
Number of cells	40	Number of 2-colour pieces	320
Number of 4-cubes	10	Number of 1-colour pieces	160
Number of 5-cubes	1	Number of 0-colour pieces	32
Number of coloured pieces	992
Number of stickers	2,560

5⁵ 5-cube

Piece count
Number of vertices	32	Number of 5-colour pieces	32
Number of edges	80	Number of 4-colour pieces	240
Number of faces	80	Number of 3-colour pieces	720
Number of cells	40	Number of 2-colour pieces	1,080
Number of 4-cubes	10	Number of 1-colour pieces	810
Number of 5-cubes	1	Number of 0-colour pieces	243
Number of coloured pieces	2,882
Number of stickers	6,250

6⁵ 5-cube

Piece count
Number of vertices	32	Number of 5-colour pieces	32
Number of edges	80	Number of 4-colour pieces	320
Number of faces	80	Number of 3-colour pieces	1,280
Number of cells	40	Number of 2-colour pieces	2,560
Number of 4-cubes	10	Number of 1-colour pieces	2,560
Number of 5-cubes	1	Number of 0-colour pieces	1,024
Number of coloured pieces	6,752
Number of stickers	12,960

7⁵ 5-cube

Piece count
Number of vertices	32	Number of 5-colour pieces	32
Number of edges	80	Number of 4-colour pieces	400
Number of faces	80	Number of 3-colour pieces	2,000
Number of cells	40	Number of 2-colour pieces	5,000
Number of 4-cubes	10	Number of 1-colour pieces	6,250
Number of 5-cubes	1	Number of 0-colour pieces	3,125
Number of coloured pieces	13,682
Number of stickers	24,010

Magic 7D Cube

Geometric shape: hexeract
Hexeract
In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces....

(6D) and hepteract
Hepteract
In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces....

(7D)

Andrey Astrelin's Magic Cube 7D software is capable of rendering puzzles of up to 7 dimensions in twelve sizes from 3⁴ to 5⁷.

As of May 2011, only 3⁶, 3⁷ and 4⁶ puzzles were solved.

Magic 120-cell

Geometric shape: 120-cell or hecatonicosachoron

The 120-cell is a 4-D geometric figure (4-polytope) composed of 120 dodecahedrons, which in turn is a 3-D figure composed of 12 pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

s. The 120-cell is the 4-D analogue of the dodecahedron in the same way that the tesseract (4-cube) is the 4-D analogue of the cube. The 4-D 120-cell software sequential move puzzle from Gravitation3d is therefore the 4-D analogue of the Megaminx

Megaminx

The Megaminx is a dodecahedron-shaped puzzle similar to the Rubik's Cube. It has a total of 50 movable pieces to rearrange, compared to the 20 movable pieces of the Rubik's cube.- History :...

dodecahedral 3-D puzzle.

The puzzle is rendered in only one size, that is three cubies on a side, but in six colouring schemes of varying difficulty. The full puzzle requires a different colour for each cell, that is 120 colours. This large number of colours adds to the difficulty of the puzzle in that some shades are quite difficult to tell apart. The easiest form is two interlocking tori, each torus forming a ring of cubies in different dimensions. The full list of colouring schemes is as follows;

2-colour tori.
9-colour 4-cube cells. That is, the same colouring scheme as the 4-cube.
9-colour layers.
12-colour rings.
60-colour antipodal. Each pair of diametrically opposed dodecahedron cells is the same colour.
120-colour full puzzle.

The controls are very similar to the 4-D Magic Cube with controls for 4-D perspective, cell size, sticker size and distance and the usual zoom and rotation. Additionally, there is the ability to completely turn off groups of cells based on selection of tori, 4-cube cells, layers or rings.

Gravitation3d has created a "Hall of Fame" for solvers, who must provide a log file for their solution. As of November 2011, the puzzle has been solved six times.

Piece count
Number of vertices	600	Number of 4-colour pieces	600
Number of edges	1,200	Number of 3-colour pieces	1,200
Number of faces	720	Number of 2-colour pieces	720
Number of cells	120	Number of 1-colour pieces	120
Number of 4-cells	1	Number of 0-colour pieces	1
Number of coloured pieces	2,640
Number of stickers	7,560

Achievable combinations:

This calculation of achievable combinations has not been mathematically proven and can only be considered an upper bound. Its derivation assumes the existence of the set of algorithms needed to make all the "minimal change" combinations. There is no reason to suppose that these algorithms will not be found since puzzle solvers have succeeded in finding them on all similar puzzles that have so far been solved.

3x3 2D square

Geometric shape: square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

Interestingly, a 2-D Rubik type puzzle can no more be physically constructed than a 4-D one can. A 3-D puzzle could be constructed with no stickers on the third dimension which would then behave as a 2-D puzzle but the true implementation of the puzzle remains in the virtual world. The implementation shown here is from Superliminal who quite perversely call it the 2D Magic Cube.

The puzzle is not of any great interest to solvers as its solution is quite trivial. In large part this is because it is not possible to put a piece in position with a twist. Some of the most difficult algorithms on the standard Rubik's cube are to deal with such twists where a piece is in its correct position but not in the correct orientation. With higher-dimension puzzles this twisting can take on the rather disconcerting form of a piece being apparently inside out. One has only to compare the difficulty of the 2×2×2 puzzle with the 3×3 (which has the same number of pieces) to see that this ability to cause twists in higher dimensions has much to do with difficulty, and hence satisfaction with solving, the ever popular Rubik's cube.

Piece count
Number of vertices	4	Number of 2-colour pieces	4
Number of edges	4	Number of 1-colour pieces	4
Number of faces	1	Number of 0-colour pieces	1
Number of coloured pieces	8
Number of stickers	12

Achievable combinations:

The centre pieces are in a fixed orientation relative to each other (in exactly the same way as the centre pieces on the standard 3×3×3 cube) and hence do not figure in the calculation of combinations.

This puzzle is not really a true 2-dimensional analogue of the Rubik's cube. If the group of operations on a single polytope of an n-dimensional puzzle is defined as any rotation of an (n – 1)-dimensional polytope in (n – 1)-dimensional space then the size of the group,

for the 5-cube is rotations of a 4-polytope in 4-space = 8×6×4 = 192,
for the 4-cube is rotations of a 3-polytope (cube) in 3-space = 6×4 = 24,
for the 3-cube is rotations of a 2-polytope (square) in 2-space = 4
for the 2-cube is rotations of a 1-polytope in 1-space = 1

In other words, the 2D puzzle cannot be scrambled at all if the same restrictions are placed on the moves as for the real 3D puzzle. The moves actually given to the 2D Magic Cube are the operations of reflection. This reflection operation can be extended to higher-dimension puzzles. For the 3D cube the analogous operation would be removing a face and replacing it with the stickers facing into the cube. For the 4-cube, the analogous operation is removing a cube and replacing it inside-out.

1D projection

Another alternate-dimension puzzle is a view achievable in David Vanderschel's 3D Magic Cube. A 4-cube projected on to a 2D computer screen is an example of a general type of an n-dimensional puzzle projected on to a (n – 2)-dimensional space. The 3D analogue of this is to project the cube on to a 1-dimensional representation, which is what Vanderschel's programme is capable of doing.

Vanderschel bewails that nobody has claimed to have solved the 1D projection of this puzzle. However, since records are not being kept for this puzzle it might not actually be the case that it is unsolved.

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Glossary