Nagata's conjecture on curves
Encyclopedia
In mathematics
, the Nagata conjecture on curves, named after Masayoshi Nagata
, governs the minimal degree required for a plane algebraic curve
to pass though a collection of very general points with prescribed multiplicity
. Nagata arrived at the conjecture via work on the 14th problem of Hilbert
, which asks whether the invariant ring of a linear group action on the polynomial ring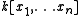
over some field 
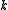is finitely generated. Nagata published the conjecture in a 1959 paper in the American Journal of Mathematics
, in which he presented a counterexample to Hilbert's 14th problem.
More precisely suppose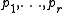
are very general points in the projective plane
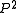and that 
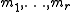are given positive integers. The Nagata conjecture states that for 
any curve 
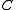in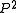 
that passes through each of the points 
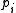with multiplicity 
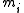must satisfy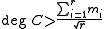
The only case when this is known to hold is when
is a perfect square (i.e. is of the form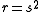 
for some integer 
), which was proved by Nagata
. Despite much interest the other cases remain open. A more modern formulation of this conjecture is often given in terms of Seshadri constant
s and has been generalised to other surfaces under the name of the Nagata–Biran conjecture.
The condition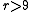
is easily seen to be necessary. The cases 
and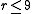 
are distinguished by whether or not the anti-canonical bundle
on the blowup
of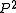
at a collection of 
points is nef
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Nagata conjecture on curves, named after Masayoshi Nagata
Masayoshi Nagata
Masayoshi Nagata was a Japanese mathematician, known for his work in the field of commutative algebra....
, governs the minimal degree required for a plane algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
to pass though a collection of very general points with prescribed multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
. Nagata arrived at the conjecture via work on the 14th problem of Hilbert
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
, which asks whether the invariant ring of a linear group action on the polynomial ring
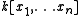over some field 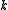is finitely generated. Nagata published the conjecture in a 1959 paper in the American Journal of MathematicsAmerican Journal of Mathematics
The American Journal of Mathematics is a bimonthly mathematics journal published by the Johns Hopkins University Press.- History :The American Journal of Mathematics is the oldest continuously-published mathematical journal in the United States, established in 1878 at the Johns Hopkins University...
, in which he presented a counterexample to Hilbert's 14th problem.
More precisely suppose
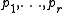are very general points in the projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
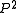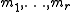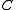and that are given positive integers. The Nagata conjecture states that for any curve in 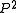that passes through each of the points 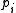with multiplicity 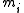must satisfy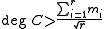The only case when this is known to hold is when
is a perfect square (i.e. is of the form 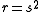for some integer ), which was proved by NagataMasayoshi Nagata
Masayoshi Nagata was a Japanese mathematician, known for his work in the field of commutative algebra....
. Despite much interest the other cases remain open. A more modern formulation of this conjecture is often given in terms of Seshadri constant
Seshadri constant
In algebraic geometry, a Seshadri constant is an invariant of an ample line bundle L at a point P on an algebraic variety. It was introduced by Demailly to measure a certain rate of growth, of the tensor powers of L, in terms of the jets of the sections of the Lk...
s and has been generalised to other surfaces under the name of the Nagata–Biran conjecture.
The condition
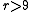is easily seen to be necessary. The cases and 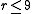are distinguished by whether or not the anti-canonical bundleCanonical bundle
In mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
on the blowup
Blowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
of
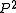at a collection of points is nefNumerically effective
A line bundle on an algebraic variety is said to be nef , if the degree of the restriction to any algebraic curve of the variety is non-negative.In particular, every ample line bundle is nef....
.