
Numerically effective
Encyclopedia
A line bundle
on an algebraic variety
is said to be nef (short for "numerically effective" or "numerically eventually free"), if the degree of the restriction to any algebraic curve
of the variety is non-negative.
In particular, every ample line bundle
is nef.
Similarly, a Cartier divisor D on an algebraic variety X is nef, if
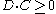
for any algebraic curve C in X, in the sense of intersection theory
.
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
on an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
is said to be nef (short for "numerically effective" or "numerically eventually free"), if the degree of the restriction to any algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of the variety is non-negative.
In particular, every ample line bundle
Ample line bundle
In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...
is nef.
Similarly, a Cartier divisor D on an algebraic variety X is nef, if
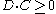
for any algebraic curve C in X, in the sense of intersection theory
Intersection theory
In mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
.

