Narrow escape problem
Encyclopedia
The narrow escape problem is a ubiquitous problem in biology, biophysics and cellular biology.
The formulation is the following: a Brownian particle
(ion
, molecule
, or protein
) is confined to a bounded domain (a compartment or a cell) by a reflecting boundary, except for a small window through which it can escape. The narrow escape problem is that of calculating the mean escape time. This time diverges as the window shrinks, thus rendering the calculation a singular perturbation
problem.
:
where
is the diffusion coefficient of the particle, 
is the friction coefficient
per unit of mass,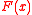
the force per unit of mass, and 
is a Brownian motion
.
before it escapes through a small absorbing window 
in its boundary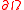 
. The time is estimated asymptotically in the limit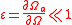 
The probability density function
(pdf)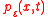
is the probability of finding the particle at position 
at time 
.
The pdf satisfies the Fokker–Planck equation
with initial condition
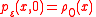
and mixed Dirichlet–Neumann boundary conditions (
)
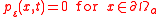
The function
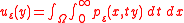
represents the mean sojourn time of particle, conditioned on the initial position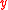
. It is the solution of the boundary value problem
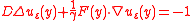
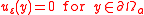
The solution depends on the dimension of the domain.
For a particle diffusing on a disk
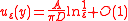
where
is the surface of the domain. The function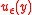 
does not depend on the initial position 
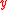, except for a small boundary layer near due to the asymptotic form.
The first order term matters in dimension 2. For a circular disk of radius
, the mean escape time of a particle starting in the center is
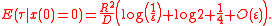
The escape time averaged with respect to a uniform initial distribution of the particle is given by
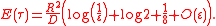
The geometry of the small opening can affect the escape time: if the
absorbing window is located at a corner of angle
, then
The formulation is the following: a Brownian particle
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
(ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
, molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
, or protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
) is confined to a bounded domain (a compartment or a cell) by a reflecting boundary, except for a small window through which it can escape. The narrow escape problem is that of calculating the mean escape time. This time diverges as the window shrinks, thus rendering the calculation a singular perturbation
Singular perturbation
In mathematics, more precisely in perturbation theory, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero...
problem.
Formulation
The motion of a particle is described by the Smoluchowski limit of the Langevin equationLangevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
:
where
is the diffusion coefficient of the particle, is the friction coefficientper unit of mass,
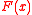the force per unit of mass, and is a Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
.
Mean first passage time
A common question is to estimate the mean sojourn time of a particle diffusing in a bounded domain before it escapes through a small absorbing window in its boundary 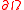. The time is estimated asymptotically in the limit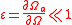 The probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(pdf)
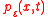is the probability of finding the particle at position at time .The pdf satisfies the Fokker–Planck equation
with initial condition
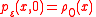
and mixed Dirichlet–Neumann boundary conditions (
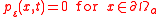
)The function
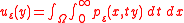
represents the mean sojourn time of particle, conditioned on the initial position
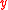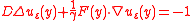
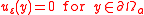
. It is the solution of the boundary value problemThe solution depends on the dimension of the domain.
For a particle diffusing on a disk
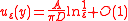
where
is the surface of the domain. The function 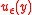does not depend on the initial position 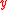, except for a small boundary layer near due to the asymptotic form.The first order term matters in dimension 2. For a circular disk of radius
, the mean escape time of a particle starting in the center is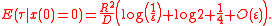The escape time averaged with respect to a uniform initial distribution of the particle is given by
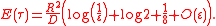
The geometry of the small opening can affect the escape time: if the
absorbing window is located at a corner of angle
, then-
More surprising, near a cusp in a two dimensional domain, the
escape time
grows algebraically, rather than
logarithmically: in the domain bounded between two tangent circles,
the escape time is
where d > 1 is the ratio of the radii. Finally, when
the domain is an annulus, the escape time to a small opening located
on the inner circle involves a second parameter which is
the ratio of the inner to the outer
radii, the escape time, averaged with respect to a uniform initial
distribution, is
-
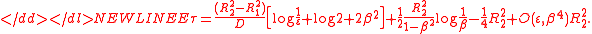
This equation contains two terms of the asymptotic expansion
of
and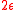 
is the angle of the absorbing
boundary. The case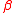
close to 1 remains open, and for general
domains, the asymptotic expansion of the escape time remains an open
problem. So does the problem of computing the escape time near a
cusp point in three-dimensional domains. For Brownian motion in a
field of force
the gap in the spectrum is not necessarily between the first and the second eigenvalues, depending
on the relative size of the small hole and force barriers the
particle has to overcome in order to escape. The escape stream is
not necessarily Poissonian.
Stochastic chemical reactions in microdomains
The forward rate of chemical reactions is the reciprocal of the narrow escape time, which generalizes the classical Smoluchowski formula for Brownian particles located in an infinite medium. A Markov description can be used to estimate the binding and unbinding to a small number of sites.
External links
-
-
