Nasik magic hypercube
Encyclopedia
A Nasik magic hypercube is a magic hypercube
with the added restriction that all possible lines through each cell sum correctly to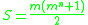
where S = the magic constant, m = the order and n = the dimension, of the hypercube.
Or, to put it more concisely, all pan-r-agonals sum correctly for r = 1...n.
The above definition is the same as the Hendricks definition of perfect, but different than the Boyer/Trump definition. See Perfect magic cube
Because of the confusion over the term perfect when used with reference to magic squares, magic cubes, and in general magic hypercubes, I am proposing the above as an unambiguous term. Following is an attempt to use the magic cube as a specific example.
A Nasik magic cube is a magic cube with the added restriction that all 13m2 possible lines sum correctly to the magic constant. This class of magic cube is commonly called perfect (John Hendricks definition.). See Magic cube classes
.
However, the term perfect is ambiguous because it is also used for other types of magic cubes. Perfect magic cube
demonstrates just one example of this.
The term nasik would apply to all dimensions of magic hypercubes in which the number of correctly summing paths (lines) through any cell of the hypercube is P = (3n- 1)/2
A pandiagonal magic square then would be a nasik square because 4 magic line pass through each of the m2cells. This was A.H. Frost’s original definition of nasik.
A nasik magic cube would have 13 magic lines passing through each of it’s m3 cells. (This cube also contains 9m pandiagonal magic squares of order m.)
A nasik magic tesseract would have 40 lines passing through each of it’s m4 cells.
And so on.
In another 1878 paper he showed another pandiagonal magic cube and a cube where all 13m lines sum correctly i.e. Hendricks perfect.
He referred to all of these cubes as nasik!
In 1905 Dr. Planck expanded on the nasik idea in his Theory of Paths Nasik. In the introductory to his paper, he wrote;
In 1917, Dr. Planck wrote again on this subject.
In 1939, B. Rosser and R. J. Walker published a series of papers on diabolic (perfect) magic squares and cubes. They specifically mentioned that these cubes contained 13m2 correctly summing lines. They also had 3m pandiagonal magic squares parallel to the faces of the cube, and 6m pandiagonal magic squares parallel to the triagonal planes.
Magic hypercubes
Magic cube
Magic cube classes
Perfect magic cube
Magic tesseract
John R. Hendricks
Categories
Magic hypercube
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares, magic cubes and magic tesseracts; that is, a number of integers arranged in an n × n × n × .....
with the added restriction that all possible lines through each cell sum correctly to
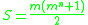where S = the magic constant, m = the order and n = the dimension, of the hypercube.Or, to put it more concisely, all pan-r-agonals sum correctly for r = 1...n.
The above definition is the same as the Hendricks definition of perfect, but different than the Boyer/Trump definition. See Perfect magic cube
Perfect magic cube
In mathematics, a perfect magic cube is a magic cube in which not only the columns, rows, pillars and main space diagonals, but also the cross section diagonals sum up to the cube's magic constant....
Because of the confusion over the term perfect when used with reference to magic squares, magic cubes, and in general magic hypercubes, I am proposing the above as an unambiguous term. Following is an attempt to use the magic cube as a specific example.
A Nasik magic cube is a magic cube with the added restriction that all 13m2 possible lines sum correctly to the magic constant. This class of magic cube is commonly called perfect (John Hendricks definition.). See Magic cube classes
Magic cube classes
Every magic cube may be assigned to one of six magic cube classes, based on the cube characteristics.This new system is more precise in defining magic cubes...
.
However, the term perfect is ambiguous because it is also used for other types of magic cubes. Perfect magic cube
Perfect magic cube
In mathematics, a perfect magic cube is a magic cube in which not only the columns, rows, pillars and main space diagonals, but also the cross section diagonals sum up to the cube's magic constant....
demonstrates just one example of this.
The term nasik would apply to all dimensions of magic hypercubes in which the number of correctly summing paths (lines) through any cell of the hypercube is P = (3n- 1)/2
A pandiagonal magic square then would be a nasik square because 4 magic line pass through each of the m2cells. This was A.H. Frost’s original definition of nasik.
A nasik magic cube would have 13 magic lines passing through each of it’s m3 cells. (This cube also contains 9m pandiagonal magic squares of order m.)
A nasik magic tesseract would have 40 lines passing through each of it’s m4 cells.
And so on.
Background support
In 1866 and 1878, Rev. A. H. Frost coined the term Nasik for the type of magic square we commonly call pandiagonal and often call perfect. He then demonstrated the concept with an order-7 cube we now class as pandiagonal, and an order-8 cube we class as pantriagonal.In another 1878 paper he showed another pandiagonal magic cube and a cube where all 13m lines sum correctly i.e. Hendricks perfect.
He referred to all of these cubes as nasik!
In 1905 Dr. Planck expanded on the nasik idea in his Theory of Paths Nasik. In the introductory to his paper, he wrote;
In 1917, Dr. Planck wrote again on this subject.
In 1939, B. Rosser and R. J. Walker published a series of papers on diabolic (perfect) magic squares and cubes. They specifically mentioned that these cubes contained 13m2 correctly summing lines. They also had 3m pandiagonal magic squares parallel to the faces of the cube, and 6m pandiagonal magic squares parallel to the triagonal planes.
Conclusion
If the term nasik is adopted as the definition for a magic hypercube where all possible lines sum correctly, there will no longer be confusion over what exactly is a Perfect magic cube. And, as in Hendricks definition of perfect, all pan-r-agonals sum correctly, and all lower dimension hypercubes contained in it are nasik (Hendricks perfect).See also
Magic hypercubeMagic hypercube
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares, magic cubes and magic tesseracts; that is, a number of integers arranged in an n × n × n × .....
Magic hypercubes
Magic cube
Magic cube
In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a number of integers arranged in a n x n x n pattern such that the sum of the numbers on each row, each column, each pillar and the four main space diagonals is equal to a single number, the so-called magic...
Magic cube classes
Magic cube classes
Every magic cube may be assigned to one of six magic cube classes, based on the cube characteristics.This new system is more precise in defining magic cubes...
Perfect magic cube
Perfect magic cube
In mathematics, a perfect magic cube is a magic cube in which not only the columns, rows, pillars and main space diagonals, but also the cross section diagonals sum up to the cube's magic constant....
Magic tesseract
Magic tesseract
In mathematics, a magic tesseract is the 4-dimensional counterpart of a magic square and magic cube, that is, a number of integers arranged in an n × n × n × n pattern such that the sum of the numbers on each pillar as well as the main space diagonals is equal to a single number,...
John R. Hendricks
External links
- History, definitions, and examples of perfect magic cubes and other dimensions.
- An alternative definition of Perfect, with history of recent discoveries
- More on this alternative definition.
- A Magic Hypercube encyclopedia with a broad range of material
- A Unified classification system for hypercubes
- An ambitious ongoing work on classifications of magic cubes and tesseracts
- A variety of John R. Hendricks material, written under his direction
Categories