Perfect magic cube - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a perfect magic cube is a magic cube

Magic cube

In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a number of integers arranged in a n x n x n pattern such that the sum of the numbers on each row, each column, each pillar and the four main space diagonals is equal to a single number, the so-called magic...

in which not only the columns, rows, pillars and main space diagonal

Space diagonal

In a rectangular box or a magic cube, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner...

s, but also the cross section

Cross section (geometry)

In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...

diagonals sum up to the cube's magic constant

Magic constant

The magic constant or magic sum of a magic square is the sum of numbers in any row, column, and diagonal of the magic square. For example, the magic square shown below has a magic constant of 15....

.

Perfect magic cubes of order one are trivial; cubes of orders two to four can be proven not to exist, and cubes of orders five and six were first discovered by Walter Trump

Walter Trump

Walter Trump is a German mathematician. He is known for discovering results on recreational mathematics.He has credits from square packing problem and magic tile problem...

and Christian Boyer on November 13 and September 1, 2003, respectively. A perfect magic cube of order seven was given by A. H. Frost in 1866, and on March 11, 1875, an article was published in the Cincinnati Commercial newspaper on the discovery of a perfect magic cube of order 8 by Gustavus Frankenstein. Perfect magic cubes of orders nine and eleven have also been constructed.
The first perfect cube of order 10 has been constructed in 1988. (Li Wen, China)

An alternative definition

In recent years, an alternative definition for the perfect magic cube was proposed by John R. Hendricks. It is based on the fact that a pandiagonal magic square has traditionally been called 'perfect', because all possible lines sum correctly. This is not the case with the above definition for the cube. See Nasik magic hypercube for an unambiguous alternative term

This same reasoning may be applied to hypercubes

Tesseract

In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

of any dimension. Simply stated; if all possible lines of m cells (m = order) sum correctly, the hypercube is perfect. All lower dimension hypercubes contained in this hypercube will then also be perfect. This is not the case with the original definition, which does not require that the planar and diagonal squares be a pandiagonal magic cube

Pandiagonal magic cube

In a Pandiagonal magic cube, all 3m planar arrays must be panmagic squares. The 6 oblique squares are always magic. Several of them may be panmagic squares....

.

The original definition is applicable only to magic cubes, not tesseracts, dimension 5 cubes, etc.

Example:
A perfect magic cube of order 8 has 244 correct lines by the old definition, but 832 correct lines by this new definition.

Order 8 is the smallest possible perfect magic cube. None can exist for double odd orders.

Gabriel Arnoux constructed an order 17 perfect magic cube in 1887. F.A.P.Barnard published order 8 and order 11 perfect cubes in 1888.

By the modern (Hendricks) definition, there are actually six classes of magic cube

Magic cube

; simple magic cube, pantriagonal magic cube

Pantriagonal magic cube

A pantriagonal magic cube is a magic cube where all 4m2 pantriagonals sum correctly. There are 4 one-segment, 12 two-segment, and 4 three-segment pantriagonals...

, diagonal magic cube

Diagonal magic cube

A Diagonal Magic Cube is an improvement over the simple magic cube. It is the second of six magic cube classes when ranked by the number of lines summing correctly....

, pantriagdiag magic cube

Pantriagdiag magic cube

A Pantriagonal Diagonal magic cube is a magic cube that is a combination Pantriagonal magic cube and Diagonal magic cube. All main and broken triagonals must sum correctly, In addition, it will contain 3m order m simple magic squares in the orthogonal planes, and 6 order m pandiagonal magic squares...

, pandiagonal magic cube

Pandiagonal magic cube

In a Pandiagonal magic cube, all 3m planar arrays must be panmagic squares. The 6 oblique squares are always magic. Several of them may be panmagic squares....

, and perfect magic cube.

Nasik; A. H. Frost (1866) referred to all but the simple magic cube as Nasik!
C. Planck (1905) redefined Nasik to mean magic hypercubes of any order or dimension in which all possible lines summed correctly.

i.e. Nasik is an alternative, and unambiguous term for the perfect class of any dimension of magic hypercube.

First known Perfect Magic Cube

Walter Trump and Christian Boyer, 2003-11-13

This cube consists of all numbers from 1 to 125.
The sum of the 5 numbers in each of the 25 rows, 25 columns, 25 pillars, 30 diagonals
and 4 triagonals (space diagonals) equals the magic constant 315.

1° level	-	2° level

3° level	-	4° level

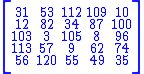5° level	-

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.