
Negation (algebra)
Encyclopedia
Negation is the mathematical operation
that reverses the sign
of a number. Thus the negation of a positive number is negative, and the negation of a negative number is positive. The negation of zero
is zero. The negation of a number , usually denoted , is often also called the opposite of .
More generally, negation may refer to any operation that replaces an object with its additive inverse
. For example, the negation of a vector is another vector with the same magnitude and the exact opposite direction.
, which can be viewed as a combination of addition
and negation:
Similarly, negation can be thought of as subtraction from zero:
Negation can also be thought of as multiplication
by negative one:
In general, double negation has no net effect on a number. That is,
for any real number
a.
This sometimes leads to somewhat confusing notation. For example, the absolute value
of a real number is usually defined by the formula: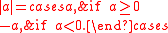
When is negative, the absolute value of is defined to be , which is always positive, being the negation of a negative number.
for that number. That is,
for any real number . (Note that is the additive identity
.)
In abstract algebra
, certain binary operation
s in algebraic structure
s are commonly written as addition
. In this case, the identity element
with respect to the binary operation is usually thought of as , and the inverse
of any element is thought of as its negation.
s by the formula
On the complex plane
, this operation rotates
a complex number 180 degrees
around the origin
.
Similarly, the negation of a Euclidean vector can be obtained by rotating the vector 180 degrees. Thus the negation of a vector has the same magnitude as the original, but the exact opposite direction. (Vectors in exactly opposite directions are sometimes referred to as antiparallel.) In terms of vector components
or more generally
Negation of vectors has the same effect as scalar multiplication
by .
In abstract algebra
, negation may refer to any operation that takes the additive inverse
of an element of an abelian group
(or any invertible element of an additive magma
).
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
that reverses the sign
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
of a number. Thus the negation of a positive number is negative, and the negation of a negative number is positive. The negation of zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
is zero. The negation of a number , usually denoted , is often also called the opposite of .
More generally, negation may refer to any operation that replaces an object with its additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
. For example, the negation of a vector is another vector with the same magnitude and the exact opposite direction.
Relation to other operations
Negation is closely related to subtractionSubtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, which can be viewed as a combination of addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and negation:
Similarly, negation can be thought of as subtraction from zero:
Negation can also be thought of as multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
by negative one:
Double negation
The negation of a negative number is positive. For example,In general, double negation has no net effect on a number. That is,
for any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
a.
This sometimes leads to somewhat confusing notation. For example, the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of a real number is usually defined by the formula:
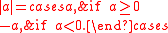
When is negative, the absolute value of is defined to be , which is always positive, being the negation of a negative number.
Additive inverse
The negation of a real number is an additive inverseAdditive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
for that number. That is,
for any real number . (Note that is the additive identity
Additive identity
In mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...
.)
In abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, certain binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s in algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s are commonly written as addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
. In this case, the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
with respect to the binary operation is usually thought of as , and the inverse
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
of any element is thought of as its negation.
Other properties
In addition to the identities listed above, negation has the following algebraic properties:Generalizations
Negation may also be defined for complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s by the formula
On the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, this operation rotates
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
a complex number 180 degrees
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
around the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
.
Similarly, the negation of a Euclidean vector can be obtained by rotating the vector 180 degrees. Thus the negation of a vector has the same magnitude as the original, but the exact opposite direction. (Vectors in exactly opposite directions are sometimes referred to as antiparallel.) In terms of vector components
or more generally
Negation of vectors has the same effect as scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
by .
In abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, negation may refer to any operation that takes the additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
of an element of an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(or any invertible element of an additive magma
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
).

