Neumann polynomial
Encyclopedia
In mathematics, a Neumanns polynomial, introduced by Carl Neumann
for the special case
, is a polynomial in 1/z used to expand functions in term of Bessel function
s.
The first few polynomials are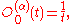
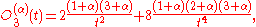
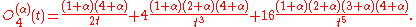
A general form for the polynomial is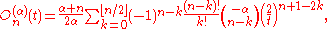
they have the generating function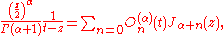
where J are Bessel function
s.
To expand a function f in form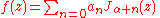
for
compute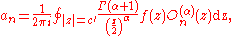
where
and c is the distance of the nearest singularity of 
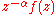from 
.
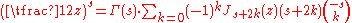
or the more general Sonine formula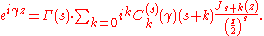
where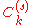
is Gegenbauer's polynomial. Then,
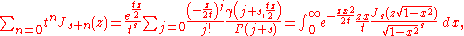
the confluent hypergeometric function
and in particular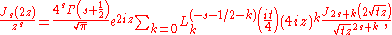
the index shift formula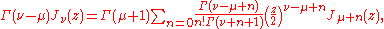
the Taylor expansion (addition formula)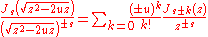
(cf. ) and the expansion of the integral of the Bessel function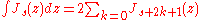
are of the same type.
Carl Neumann
Carl Gottfried Neumann was a German mathematician.Neumann was born in Königsberg, Prussia, as the son of the mineralogist, physicist and mathematician Franz Ernst Neumann , who was professor of mineralogy and physics at Königsberg University...
for the special case
, is a polynomial in 1/z used to expand functions in term of Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s.
The first few polynomials are
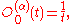
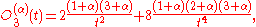
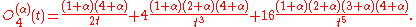
A general form for the polynomial is
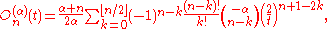
they have the generating function
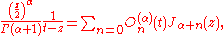
where J are Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s.
To expand a function f in form
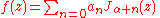
for
compute
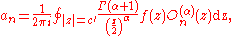
where
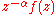and c is the distance of the nearest singularity of from .Examples
An example is the extension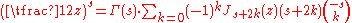or the more general Sonine formula
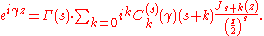
where
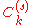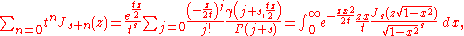
is Gegenbauer's polynomial. Then,the confluent hypergeometric function
Confluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
and in particular
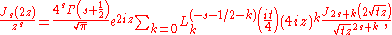
the index shift formula
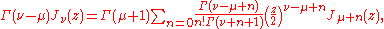
the Taylor expansion (addition formula)
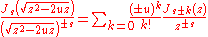
(cf. ) and the expansion of the integral of the Bessel function
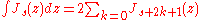
are of the same type.
See also
- Bessel functionBessel functionIn mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
- Lommel polynomial
- Hankel transformHankel transformIn mathematics, the Hankel transform expresses any given function f as the weighted sum of an infinite number of Bessel functions of the first kind Jν. The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r-axis...
- Fourier–Bessel series