
Hankel transform
Encyclopedia
In mathematics
, the Hankel transform expresses any given function f(r) as the weighted sum of an infinite number of Bessel functions of the first kind Jν(kr). The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r-axis. The necessary coefficient Fν of each Bessel function in the sum, as a function of the scaling factor k constitutes the transformed function.
More precisely, the Hankel transform of order ν of a function f(r) is given by:
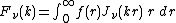
where Jν is the Bessel function
of the first kind of order ν with ν ≥ −1/2. The inverse Hankel transform of Fν(k) is defined as:
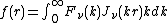
which can be readily verified using the orthogonality relationship described below.
The Hankel transform is an integral transform and was first developed by the mathematician Hermann Hankel
. It is also known as the Fourier–Bessel transform. Just as the Fourier transform
for an infinite interval is related to the Fourier series
over a finite interval, so the Hankel transform over an infinite interval is related to the Fourier–Bessel series over a finite interval.
f(r) is continuous provided that the function is defined in (0, ∞), is piecewise continuous and of bounded variation in every finite subinterval in (0, ∞), and the integral
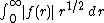
is finite. However, like the Fourier Transform, the domain can be extended by a density argument to include some functions whose above integral is not finite, for example ; this extension will not be discussed in this article.
; this extension will not be discussed in this article.
with respect
to the weighting factor r:
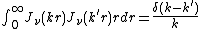
for k and k greater than zero.
well defined, then the Plancherel theorem
states
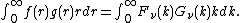
Parseval's theorem
, which states:
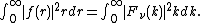
is a special case of the Plancherel theorem. These theorems can be proven using the orthogonality property.
Fourier transform
of a circularly symmetric function.
Consider a two-dimensional function f(r) of the radius vector r.
Its Fourier transform is:
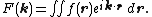
With no loss of generality, we can pick a polar coordinate system (r, θ) such
that the k vector lies on the θ = 0 axis. The Fourier transform is now written in these polar coordinates as:
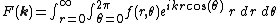
where θ is the angle between the k and r vectors. If the
function f happens to be circularly symmetric, it will have no dependence on
the angular variable θ and may be written f(r). The integration over θ may be carried out, and the Fourier transform is now written:

which is just 2π times the zero-order Hankel transform of f(r). For the reverse transform,
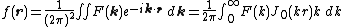
so f(r) is 1/2π times the zero-order Hankel transform of F(k).
To generalize: If f is expanded
in a multipole series
,
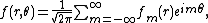
and if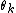 is the angle between the direction of k
is the angle between the direction of k
and the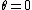 axis,
axis,
 ,
,
one may substitute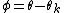 ,
,
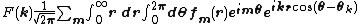
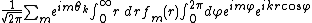
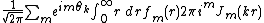
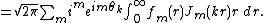
If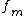 is sufficiently smooth near the origin
is sufficiently smooth near the origin
and zero outside a radius
 , it may be expanded into a Chebyshev series
, it may be expanded into a Chebyshev series
,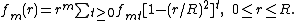
The numerically important aspect is that
the expansion coefficients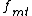 are accessible with
are accessible with
Discrete Fourier transform
techniques. Insertion into the previous formula
yields
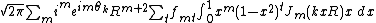

This is one flavor of fast Hankel transform techniques.
of integral operators. In two dimensions, if we define A as the Abel transform
operator, F as the Fourier transform
operator and H as the zeroth order Hankel transform operator, then the special case of the projection-slice theorem
for circularly symmetric functions states that:
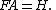
In other words, applying the Abel transform to a 1-dimensional function and
then applying the Fourier transform to that result is the same as applying
the Hankel transform to that function. This concept can be extended to higher
dimensions.
}{k}=\sqrt{\frac{2|z|}{\pi k}}K_{-1/2}(k|z|)\,
|-
|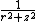
|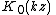 , z may be any complex number
, z may be any complex number
|-
|
|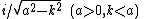
|-
|
|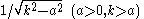
|-
|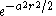
|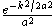
|-
|
|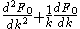
|-
!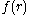
!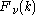
|-
|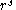
|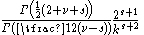
|-
|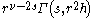
|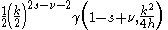
|-
|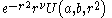
|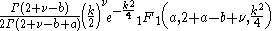
|-
|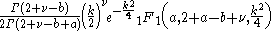
|
|}
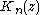 is a modified Bessel function of the second kind.
is a modified Bessel function of the second kind.
The expression
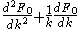
coincides with the expression
for the Laplace operator
in polar coordinates
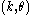
applied to a spherically symmetric function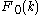 .
.
The Hankel transform of Zernike polynomials are essentially
Bessel Functions (Noll 1976):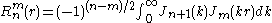
for even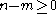 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hankel transform expresses any given function f(r) as the weighted sum of an infinite number of Bessel functions of the first kind Jν(kr). The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r-axis. The necessary coefficient Fν of each Bessel function in the sum, as a function of the scaling factor k constitutes the transformed function.
More precisely, the Hankel transform of order ν of a function f(r) is given by:
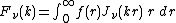
where Jν is the Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind of order ν with ν ≥ −1/2. The inverse Hankel transform of Fν(k) is defined as:
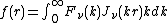
which can be readily verified using the orthogonality relationship described below.
The Hankel transform is an integral transform and was first developed by the mathematician Hermann Hankel
Hermann Hankel
Hermann Hankel was a German mathematician who was born in Halle, Germany and died in Schramberg , Imperial Germany....
. It is also known as the Fourier–Bessel transform. Just as the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
for an infinite interval is related to the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
over a finite interval, so the Hankel transform over an infinite interval is related to the Fourier–Bessel series over a finite interval.
Domain of definition
The Hankel transform of a function f(r) is valid at every point at whichf(r) is continuous provided that the function is defined in (0, ∞), is piecewise continuous and of bounded variation in every finite subinterval in (0, ∞), and the integral
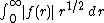
is finite. However, like the Fourier Transform, the domain can be extended by a density argument to include some functions whose above integral is not finite, for example
 ; this extension will not be discussed in this article.
; this extension will not be discussed in this article.Orthogonality
The Bessel functions form an orthogonal basisOrthogonal basis
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
with respect
to the weighting factor r:
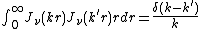
for k and k greater than zero.
The Plancherel theorem and Parseval's theorem
If f(r) and g(r) are such that their Hankel transforms Fν(k) and Gν(k) arewell defined, then the Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
states
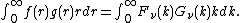
Parseval's theorem
Parseval's theorem
In mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum of the square of a function is equal to the sum of the square of its transform. It originates from a 1799 theorem about series by Marc-Antoine Parseval, which was later...
, which states:
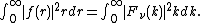
is a special case of the Plancherel theorem. These theorems can be proven using the orthogonality property.
Relation to the Fourier transform
The Hankel transform of order zero is essentially the two dimensionalFourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of a circularly symmetric function.
Consider a two-dimensional function f(r) of the radius vector r.
Its Fourier transform is:
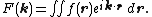
With no loss of generality, we can pick a polar coordinate system (r, θ) such
that the k vector lies on the θ = 0 axis. The Fourier transform is now written in these polar coordinates as:
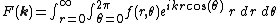
where θ is the angle between the k and r vectors. If the
function f happens to be circularly symmetric, it will have no dependence on
the angular variable θ and may be written f(r). The integration over θ may be carried out, and the Fourier transform is now written:

which is just 2π times the zero-order Hankel transform of f(r). For the reverse transform,
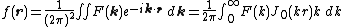
so f(r) is 1/2π times the zero-order Hankel transform of F(k).
To generalize: If f is expanded
in a multipole series
Multipole expansion
A multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
,
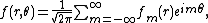
and if
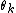 is the angle between the direction of k
is the angle between the direction of kand the
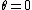 axis,
axis, ,
,one may substitute
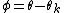 ,
,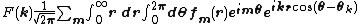
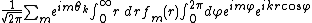
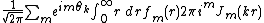
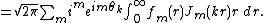
If
 is sufficiently smooth near the origin
is sufficiently smooth near the originand zero outside a radius
 , it may be expanded into a Chebyshev series
, it may be expanded into a Chebyshev seriesChebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
,
The numerically important aspect is that
the expansion coefficients
 are accessible with
are accessible withDiscrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
techniques. Insertion into the previous formula
yields

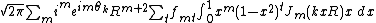

This is one flavor of fast Hankel transform techniques.
Relation to the Fourier and Abel transforms
The Hankel transform is one member of the FHA cycleProjection-slice theorem
In mathematics, the projection-slice theorem or Fourier slice theorem in two dimensions states that the results of the following two calculations are equal:...
of integral operators. In two dimensions, if we define A as the Abel transform
Abel transform
In mathematics, the Abel transform, named for Niels Henrik Abel, is an integral transform often used in the analysis of spherically symmetric or axially symmetric functions...
operator, F as the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
operator and H as the zeroth order Hankel transform operator, then the special case of the projection-slice theorem
Projection-slice theorem
In mathematics, the projection-slice theorem or Fourier slice theorem in two dimensions states that the results of the following two calculations are equal:...
for circularly symmetric functions states that:
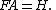
In other words, applying the Abel transform to a 1-dimensional function and
then applying the Fourier transform to that result is the same as applying
the Hankel transform to that function. This concept can be extended to higher
dimensions.
Some Hankel transform pairs
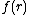 |
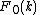 |
|---|---|
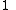 |
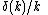 |
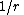 |
 |
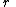 |
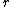 |
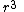 |
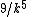 |
 |
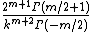 for m odd for m odd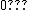 for m even for m even |
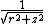 |
|-
|
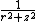
|
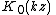 , z may be any complex number
, z may be any complex number|-
|

|
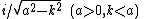
|-
|

|
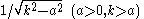
|-
|
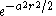
|
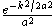
|-
|

|
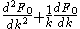
|-
!
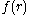
!
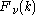
|-
|
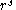
|
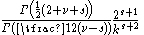
|-
|
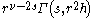
|
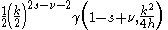
|-
|
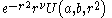
|
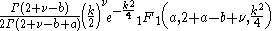
|-
|
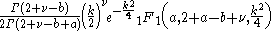
|

|}
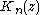 is a modified Bessel function of the second kind.
is a modified Bessel function of the second kind.The expression
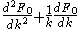
coincides with the expression
for the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
in polar coordinates
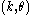
applied to a spherically symmetric function
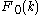 .
.The Hankel transform of Zernike polynomials are essentially
Bessel Functions (Noll 1976):
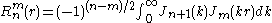
for even
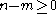 .
.See also
- Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
- Integral transform
- Abel transformAbel transformIn mathematics, the Abel transform, named for Niels Henrik Abel, is an integral transform often used in the analysis of spherically symmetric or axially symmetric functions...
- Fourier–Bessel series
- Neumann polynomialNeumann polynomialIn mathematics, a Neumanns polynomial, introduced by Carl Neumann for the special case \alpha=0, is a polynomial in 1/z used to expand functions in term of Bessel functions....

