
Projection-slice theorem
Encyclopedia
In mathematics
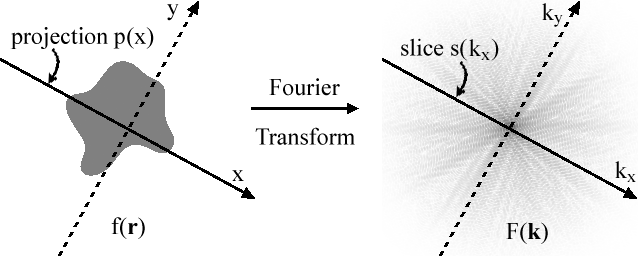
, the projection-slice theorem or Fourier slice theorem in two dimensions states that the results of the following two calculations are equal:
In operator terms, if
then:
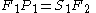
This idea can be extended to higher dimensions.
This theorem is used, for example, in the analysis of medical
CT scans where a "projection" is an x-ray
image of an internal organ. The Fourier transforms of these images are
seen to be slices through the Fourier transform of the 3-dimensional
density of the internal organ, and these slices can be interpolated to build
up a complete Fourier transform of that density. The inverse Fourier transform
is then used to recover the 3-dimensional density of the object. This technique was first derived by Bracewell (1956) for a radio astronomy problem
Fourier transform
of the projection of an N-dimensional function
f(r) onto an m-dimensional linear submanifold
is equal to an m-dimensional slice of the N-dimensional Fourier transform of that
function consisting of an m-dimensional linear submanifold through the origin in the Fourier space which is parallel to the projection submanifold. In operator terms:
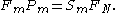
 The projection-slice theorem is easily proven for the case of two dimensions.
The projection-slice theorem is easily proven for the case of two dimensions.
Without loss of generality, we can take the projection line to be the x-axis.
There is no loss of generality because using a shifted and rotated line the law still applies. Using a shifted line (in y) gives the same projection and therefore the same 1D Fourier transform. Rotated function is the Fourier pair of the rotated Fourier transform, this completes the explanation.
If f(x, y) is a two-dimensional function, then the projection of f(x) onto the x axis is p(x) where

The Fourier transform of is
is
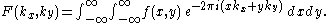
The slice is then

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the projection-slice theorem or Fourier slice theorem in two dimensions states that the results of the following two calculations are equal:
- Take a two-dimensional function f(r), projectProjection (mathematics)Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
it onto a (one-dimensional) line, and do a Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of that projection. - Take that same function, but do a two-dimensional Fourier transform first, and then slice it through its origin, which is parallel to the projection line.
In operator terms, if
- F1 and F2 are the 1- and 2-dimensional Fourier transform operators mentioned above,
- P1 is the projection operator (which projects a 2-D function onto a 1-D line) and
- S1 is a slice operator (which extracts a 1-D central slice from a function),
then:
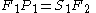
This idea can be extended to higher dimensions.
This theorem is used, for example, in the analysis of medical
CT scans where a "projection" is an x-ray
image of an internal organ. The Fourier transforms of these images are
seen to be slices through the Fourier transform of the 3-dimensional
density of the internal organ, and these slices can be interpolated to build
up a complete Fourier transform of that density. The inverse Fourier transform
is then used to recover the 3-dimensional density of the object. This technique was first derived by Bracewell (1956) for a radio astronomy problem
The projection-slice theorem in N dimensions
In N dimensions, the projection-slice theorem states that theFourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the projection of an N-dimensional function
f(r) onto an m-dimensional linear submanifold
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is equal to an m-dimensional slice of the N-dimensional Fourier transform of that
function consisting of an m-dimensional linear submanifold through the origin in the Fourier space which is parallel to the projection submanifold. In operator terms:
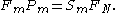
Proof in two dimensions

Without loss of generality, we can take the projection line to be the x-axis.
There is no loss of generality because using a shifted and rotated line the law still applies. Using a shifted line (in y) gives the same projection and therefore the same 1D Fourier transform. Rotated function is the Fourier pair of the rotated Fourier transform, this completes the explanation.
If f(x, y) is a two-dimensional function, then the projection of f(x) onto the x axis is p(x) where

The Fourier transform of
 is
is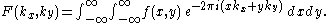
The slice is then


-
-

-
-
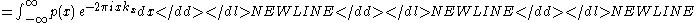
which is just the Fourier transform of p(x). The proof for higher dimensions is easily generalized from the above example.
The FHA cycle
If the two-dimensional function f(r) is circularly symmetric, it may be represented as f(r) where r = |r|. In this case the projection onto any projection line
will be the Abel transformAbel transformIn mathematics, the Abel transform, named for Niels Henrik Abel, is an integral transform often used in the analysis of spherically symmetric or axially symmetric functions...
of f(r). The two-dimensional Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of f(r) will be a circularly symmetric function given by the zeroth order Hankel transformHankel transformIn mathematics, the Hankel transform expresses any given function f as the weighted sum of an infinite number of Bessel functions of the first kind Jν. The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r-axis...
of f(r), which will therefore also represent any slice through the origin. The projection-slice theorem then states that the Fourier transform of the projection equals the slice or
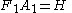
where A1 represents the Abel transform operator, projecting a two-dimensional circularly symmetric function onto a one-dimensional line, F1 represents the 1-D Fourier transform
operator, and H represents the zeroth order Hankel transform operator.
Extension to n-dimension signal
The n-dimensional projection-slice theorm has been developed by Ng in 2005 for the application of digital refocusing.
-
-
-

