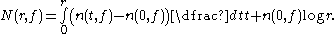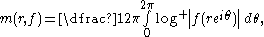Nevanlinna theory
Encyclopedia
Nevanlinna theory is a branch of complex analysis
developed by Rolf Nevanlinna
. It deals with the value distribution theory of holomorphic functions
in one variable, usually denoted z.
Nevanlinna theory is very useful when dealing with meromorphic function
s as their poles can block attempts at analysis by more conventional means such as the maximum modulus principle
.
This function, known as the N function, counts the poles of f. We further define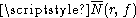
as counting the poles without regards to multiplicity.
We now define the second Nevanlinna functional:
and hence the Nevanlinna characteristic function:
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
developed by Rolf Nevanlinna
Rolf Nevanlinna
Rolf Herman Nevanlinna was one of the most famous Finnish mathematicians. He was particularly appreciated for his work in complex analysis.- The Nevanlinna family :...
. It deals with the value distribution theory of holomorphic functions
Value distribution theory of holomorphic functions
In mathematics, the value distribution theory of holomorphic functions is a division of mathematical analysis. It tries to get quantitative measures of the number of times a function f assumes a value a, as z grows in size, refining the Picard theorem on behaviour close to an essential singularity...
in one variable, usually denoted z.
Nevanlinna theory is very useful when dealing with meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s as their poles can block attempts at analysis by more conventional means such as the maximum modulus principle
Maximum modulus principle
In mathematics, the maximum modulus principle in complex analysis states that if f is a holomorphic function, then the modulus |f| cannot exhibit a true local maximum that is properly within the domain of f....
.
Basic definitions
We first define n(r, ƒ) to be the number of poles of ƒ in the disc |z| < r, with regards to multiplicity — i.e. a double pole will add 2 to n(r, ƒ) and a simple pole will add 1. Hence we set:
This function, known as the N function, counts the poles of f. We further define
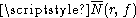as counting the poles without regards to multiplicity.We now define the second Nevanlinna functional:
and hence the Nevanlinna characteristic function:
