Newton's law of universal gravitation
Encyclopedia
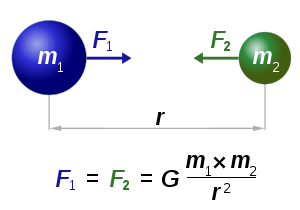
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. (Separately it was shown that large spherically symmetrical masses attract and are attracted as if all their mass were concentrated at their centers.
) This is a general physical law
derived from empirical
observations by what Newton
called induction. It is a part of classical mechanics
and was formulated in Newton's work Philosophiae Naturalis Principia Mathematica
("the Principia"), first published on 5 July 1687. (When Newton's book was presented in 1686 to the Royal Society
, Robert Hooke
made a claim that Newton had obtained the inverse square law from him – see History section below.)
In modern language, the law states the following:
Assuming SI units
, F is measured in newtons (N), m1 and m2 in kilogram
s (kg), r in meters (m), and the constant G is approximately equal to .
The value of the constant G was first accurately determined from the results of the Cavendish experiment
conducted by the British
scientist Henry Cavendish
in 1798, although Cavendish did not himself calculate a numerical value for G. This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force.
Newton's law of gravitation resembles Coulomb's law
of electrical forces, which is used to calculate the magnitude of electrical force between two charged bodies. Both are inverse-square law
s, in which force is inversely proportional to the square of the distance between the bodies. Coulomb's Law has the product of two charges in place of the product of the masses, and the electrostatic constant in place of the gravitational constant.
Newton's law has since been superseded by Einstein's theory of general relativity
, but it continues to be used as an excellent approximation of the effects of gravity. Relativity is required only when there is a need for extreme precision, or when dealing with gravitation for extremely massive and dense objects.
's Principia
was presented to the Royal Society
, Robert Hooke
accused Newton of plagiarism
by claiming that he had taken from him the "notion" of "the rule of the decrease of Gravity, being reciprocally as the squares of the distances from the Center". At the same time (according to Edmond Halley
's contemporary report) Hooke agreed that "the Demonstration of the Curves generated thereby" was wholly Newton's.
In this way arose the question what, if anything, did Newton owe to Hooke? – a subject extensively discussed since that time, and on which some points still excite some controversy.
Hooke's statements up to 1674 made no mention, however, that an inverse square law applies or might apply to these attractions. Hooke's gravitation was also not yet universal, though it approached universality more closely than previous hypotheses. He also did not provide accompanying evidence or mathematical demonstration. On the latter two aspects, Hooke himself stated in 1674: "Now what these several degrees [of attraction] are I have not yet experimentally verified"; and as to his whole proposal: "This I only hint at present", "having my self many other things in hand which I would first compleat, and therefore cannot so well attend it" (i.e. "prosecuting this Inquiry"). It was later on, in writing on 6 January 1679|80 to Newton, that Hooke communicated his "supposition ... that the Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall, and Consequently that the Velocity will be in a subduplicate proportion to the Attraction and Consequently as Kepler Supposes Reciprocall to the Distance." (The inference about the velocity was incorrect.)
Hooke's correspondence of 1679-1680 with Newton mentioned not only this inverse square supposition for the decline of attraction with increasing distance, but also, in Hooke's opening letter to Newton, of 24 November 1679, an approach of "compounding the celestial motions of the planetts of a direct motion by the tangent & an attractive motion towards the central body".
, (who suggested, but without demonstration, that there was an attractive force from the Sun in the inverse square proportion to the distance), and Borelli
(who suggested, also without demonstration, that there was a centrifugal tendency in counterbalance with a gravitational attraction towards the Sun so as to make the planets move in ellipses). D T Whiteside has described the contribution to Newton's thinking that came from Borelli's book, a copy of which was in Newton's library at his death.
Newton further defended his work by saying that had he first heard of the inverse square proportion from Hooke, he would still have some rights to it in view of his demonstrations of its accuracy. Hooke, without evidence in favor of the supposition, could only guess that the inverse square law was approximately valid at great distances from the center. According to Newton, while the 'Principia' was still at pre-publication stage, there were so many a-priori reasons to doubt the accuracy of the inverse-square law (especially close to an attracting sphere) that "without my (Newton's) Demonstrations, to which Mr Hook is yet a stranger, it cannot be by a judicious Philosopher to be any where accurate."
This remark refers among other things to Newton's finding, supported by mathematical demonstration, that if the inverse square law applies to tiny particles, then even a large spherically symmetrical mass also attracts masses external to its surface, even close up, exactly as if all its own mass were concentrated at its center. Thus Newton gave a justification, otherwise lacking, for applying the inverse square law to large spherical planetary masses as if they were tiny particles. In addition, Newton had formulated in Propositions 43-45 of Book 1, and associated sections of Book 3, a sensitive test of the accuracy of the inverse square law, in which he showed that only where the law of force is accurately as the inverse square of the distance will the directions of orientation of the planets' orbital ellipses stay constant as they are observed to do apart from small effects attributable to inter-planetary perturbations.
In regard to evidence that still survives of the earlier history, manuscripts written by Newton in the 1660s show that Newton himself had arrived by 1669 at proofs that in a circular case of planetary motion, 'endeavour to recede' (what was later called centrifugal force) had an inverse-square relation with distance from the center. After his 1679-1680 correspondence with Hooke, Newton adopted the language of inward or centripetal force. According to Newton scholar J Bruce Brackenridge, although much has been made of the change in language and difference of point of view, as between centrifugal or centripetal forces, the actual computations and proofs remained the same either way. They also involved the combination of tangential and radial displacements, which Newton was making in the 1660s. The lesson offered by Hooke to Newton here, although significant, was one of perspective and did not change the analysis. This background shows there was basis for Newton to deny deriving the inverse square law from Hooke.
Nevertheless, a number of authors have had more to say about what Newton gained from Hooke and some aspects remain controversial. The fact that most of Hooke's private papers had been destroyed or disappeared does not help to establish the truth.
Newton's role in relation to the inverse square law was not as it has sometimes been represented, he did not claim to think it up as a bare idea. What Newton did was to show how the inverse-square law of attraction had many necessary mathematical connections with observable features of the motions of bodies in the solar system; and that they were related in such a way that the observational evidence and the mathematical demonstrations, taken together, gave reason to believe that the inverse square law was not just approximately true but exactly true (to the accuracy achievable in Newton's time and for about two centuries afterwards – and with some loose ends of points that could not yet be certainly examined, where the implications of the theory had not yet been adequately identified or calculated).
In the light of the background described above, it becomes understandable how, about thirty years after Newton's death in 1727, Alexis Clairaut, a mathematical astronomer eminent in his own right in the field of gravitational studies, wrote after reviewing what Hooke published, that "One must not think that this idea ... of Hooke diminishes Newton's glory"; and that "the example of Hooke" serves "to show what a distance there is between a truth that is glimpsed and a truth that is demonstrated".
the force (in vector form, see below) over the extents of the two bodies
.
In this way it can be shown that an object with a spherically-symmetric distribution of mass exerts the same gravitational attraction on external bodies as if all the object's mass were concentrated at a point at its centre. (This is not generally true for non-spherically-symmetrical bodies.)
For points inside a spherically-symmetric distribution of matter, Newton's Shell theorem
can be used to find the gravitational force. The theorem tells us how different parts of the mass distribution affect the gravitational force measured at a point located a distance r0 from the center of the mass distribution:
As a consequence, for example, within a shell of uniform thickness and density there is no net gravitational acceleration anywhere within the hollow sphere.
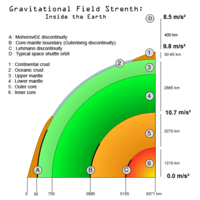Furthermore, inside a uniform sphere the gravity increases linearly with the distance from the center; the increase due to the additional mass is 1.5 times the decrease due to the larger distance from the center. Thus, if a spherically symmetric body has a uniform core and a uniform mantle with a density that is less than 2/3 of that of the core, then the gravity initially decreases outwardly beyond the boundary, and if the sphere is large enough, further outward the gravity increases again, and eventually it exceeds the gravity at the core/mantle boundary. The gravity of the Earth may be highest at the core/mantle boundary.
Newton's law of universal gravitation can be written as a vector equation
to account for the direction of the gravitational force as well as its magnitude. In this formula, quantities in bold represent vectors.
Shell theorem
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
) This is a general physical law
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
derived from empirical
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
observations by what Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
called induction. It is a part of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and was formulated in Newton's work Philosophiae Naturalis Principia Mathematica
Philosophiae Naturalis Principia Mathematica
Philosophiæ Naturalis Principia Mathematica, Latin for "Mathematical Principles of Natural Philosophy", often referred to as simply the Principia, is a work in three books by Sir Isaac Newton, first published 5 July 1687. Newton also published two further editions, in 1713 and 1726...
("the Principia"), first published on 5 July 1687. (When Newton's book was presented in 1686 to the Royal Society
Royal Society
The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...
, Robert Hooke
Robert Hooke
Robert Hooke FRS was an English natural philosopher, architect and polymath.His adult life comprised three distinct periods: as a scientific inquirer lacking money; achieving great wealth and standing through his reputation for hard work and scrupulous honesty following the great fire of 1666, but...
made a claim that Newton had obtained the inverse square law from him – see History section below.)
In modern language, the law states the following:
| Every point mass attracts every single other point mass by a force Force In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform... pointing along the line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects... intersecting both points. The force is proportional Proportionality (mathematics) In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one... to the product Product (mathematics) In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication... of the two mass Mass Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:... es and inversely proportional Proportionality (mathematics) In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one... to the square of the distance between them: |
|
 ,where:
|
 |
Assuming SI units
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
, F is measured in newtons (N), m1 and m2 in kilogram
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
s (kg), r in meters (m), and the constant G is approximately equal to .
The value of the constant G was first accurately determined from the results of the Cavendish experiment
Cavendish experiment
The Cavendish experiment, performed in 1797–98 by British scientist Henry Cavendish was the first experiment to measure the force of gravity between masses in the laboratory, and the first to yield accurate values for the gravitational constant. Because of the unit conventions then in use,...
conducted by the British
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
scientist Henry Cavendish
Henry Cavendish
Henry Cavendish FRS was a British scientist noted for his discovery of hydrogen or what he called "inflammable air". He described the density of inflammable air, which formed water on combustion, in a 1766 paper "On Factitious Airs". Antoine Lavoisier later reproduced Cavendish's experiment and...
in 1798, although Cavendish did not himself calculate a numerical value for G. This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force.
Newton's law of gravitation resembles Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
of electrical forces, which is used to calculate the magnitude of electrical force between two charged bodies. Both are inverse-square law
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
s, in which force is inversely proportional to the square of the distance between the bodies. Coulomb's Law has the product of two charges in place of the product of the masses, and the electrostatic constant in place of the gravitational constant.
Newton's law has since been superseded by Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, but it continues to be used as an excellent approximation of the effects of gravity. Relativity is required only when there is a need for extreme precision, or when dealing with gravitation for extremely massive and dense objects.
Early history
A recent assessment (by Ofer Gal) about the early history of the inverse square law is that "by the late 1660s," the assumption of an "inverse proportion between gravity and the square of distance was rather common and had been advanced by a number of different people for different reasons". The same author does credit Hooke with a significant and even seminal contribution, but he treats Hooke's claim of priority on the inverse square point as uninteresting since several individuals besides Newton and Hooke had at least suggested it, and he points instead to the idea of "compounding the celestial motions" and the conversion of Newton's thinking away from 'centrifugal' and towards 'centripetal' force as Hooke's significant contributions.Plagiarism dispute
In 1686, when the first book of NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's Principia
Philosophiae Naturalis Principia Mathematica
Philosophiæ Naturalis Principia Mathematica, Latin for "Mathematical Principles of Natural Philosophy", often referred to as simply the Principia, is a work in three books by Sir Isaac Newton, first published 5 July 1687. Newton also published two further editions, in 1713 and 1726...
was presented to the Royal Society
Royal Society
The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...
, Robert Hooke
Robert Hooke
Robert Hooke FRS was an English natural philosopher, architect and polymath.His adult life comprised three distinct periods: as a scientific inquirer lacking money; achieving great wealth and standing through his reputation for hard work and scrupulous honesty following the great fire of 1666, but...
accused Newton of plagiarism
Plagiarism
Plagiarism is defined in dictionaries as the "wrongful appropriation," "close imitation," or "purloining and publication" of another author's "language, thoughts, ideas, or expressions," and the representation of them as one's own original work, but the notion remains problematic with nebulous...
by claiming that he had taken from him the "notion" of "the rule of the decrease of Gravity, being reciprocally as the squares of the distances from the Center". At the same time (according to Edmond Halley
Edmond Halley
Edmond Halley FRS was an English astronomer, geophysicist, mathematician, meteorologist, and physicist who is best known for computing the orbit of the eponymous Halley's Comet. He was the second Astronomer Royal in Britain, following in the footsteps of John Flamsteed.-Biography and career:Halley...
's contemporary report) Hooke agreed that "the Demonstration of the Curves generated thereby" was wholly Newton's.
In this way arose the question what, if anything, did Newton owe to Hooke? – a subject extensively discussed since that time, and on which some points still excite some controversy.
Hooke's work and claims
Robert Hooke published his ideas about the "System of the World" in the 1660s, when he read to the Royal Society on 21 March 1666 a paper "On gravity", "concerning the inflection of a direct motion into a curve by a supervening attractive principle", and he published them again in somewhat developed form in 1674, as an addition to "An Attempt to Prove the Motion of the Earth from Observations". Hooke announced in 1674 that he planned to "explain a System of the World differing in many particulars from any yet known", based on three "Suppositions": that "all Coelestial Bodies whatsoever, have an attraction or gravitating power towards their own Centers" [and] "they do also attract all the other Coelestial Bodies that are within the sphere of their activity"; that "all bodies whatsoever that are put into a direct and simple motion, will so continue to move forward in a straight line, till they are by some other effectual powers deflected and bent..."; and that "these attractive powers are so much the more powerful in operating, by how much the nearer the body wrought upon is to their own Centers". Thus Hooke clearly postulated mutual attractions between the Sun and planets, in a way that increased with nearness to the attracting body, together with a principle of linear inertia.Hooke's statements up to 1674 made no mention, however, that an inverse square law applies or might apply to these attractions. Hooke's gravitation was also not yet universal, though it approached universality more closely than previous hypotheses. He also did not provide accompanying evidence or mathematical demonstration. On the latter two aspects, Hooke himself stated in 1674: "Now what these several degrees [of attraction] are I have not yet experimentally verified"; and as to his whole proposal: "This I only hint at present", "having my self many other things in hand which I would first compleat, and therefore cannot so well attend it" (i.e. "prosecuting this Inquiry"). It was later on, in writing on 6 January 1679|80 to Newton, that Hooke communicated his "supposition ... that the Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall, and Consequently that the Velocity will be in a subduplicate proportion to the Attraction and Consequently as Kepler Supposes Reciprocall to the Distance." (The inference about the velocity was incorrect.)
Hooke's correspondence of 1679-1680 with Newton mentioned not only this inverse square supposition for the decline of attraction with increasing distance, but also, in Hooke's opening letter to Newton, of 24 November 1679, an approach of "compounding the celestial motions of the planetts of a direct motion by the tangent & an attractive motion towards the central body".
Newton's work and claims
Newton, faced in May 1686 with Hooke's claim on the inverse square law, denied that Hooke was to be credited as author of the idea. Among the reasons, Newton recalled that the idea had been discussed with Sir Christopher Wren previous to Hooke's 1679 letter. Newton also pointed out and acknowledged prior work of others, including BullialdusIsmaël Bullialdus
Ismaël Bullialdus was a French astronomer.Bullialdus was born Ismaël Boulliau in Loudun, Vienne, France, the first surviving son to Calvinists Susanna Motet and Ismaël Boulliau, a notary by profession and amateur astronomer. At age twenty-one he converted to Catholicism, and by twenty-six was...
, (who suggested, but without demonstration, that there was an attractive force from the Sun in the inverse square proportion to the distance), and Borelli
Giovanni Alfonso Borelli
Giovanni Alfonso Borelli was a Renaissance Italian physiologist, physicist, and mathematician. He contributed to the modern principle of scientific investigation by continuing Galileo's custom of testing hypotheses against observation...
(who suggested, also without demonstration, that there was a centrifugal tendency in counterbalance with a gravitational attraction towards the Sun so as to make the planets move in ellipses). D T Whiteside has described the contribution to Newton's thinking that came from Borelli's book, a copy of which was in Newton's library at his death.
Newton further defended his work by saying that had he first heard of the inverse square proportion from Hooke, he would still have some rights to it in view of his demonstrations of its accuracy. Hooke, without evidence in favor of the supposition, could only guess that the inverse square law was approximately valid at great distances from the center. According to Newton, while the 'Principia' was still at pre-publication stage, there were so many a-priori reasons to doubt the accuracy of the inverse-square law (especially close to an attracting sphere) that "without my (Newton's) Demonstrations, to which Mr Hook is yet a stranger, it cannot be by a judicious Philosopher to be any where accurate."
This remark refers among other things to Newton's finding, supported by mathematical demonstration, that if the inverse square law applies to tiny particles, then even a large spherically symmetrical mass also attracts masses external to its surface, even close up, exactly as if all its own mass were concentrated at its center. Thus Newton gave a justification, otherwise lacking, for applying the inverse square law to large spherical planetary masses as if they were tiny particles. In addition, Newton had formulated in Propositions 43-45 of Book 1, and associated sections of Book 3, a sensitive test of the accuracy of the inverse square law, in which he showed that only where the law of force is accurately as the inverse square of the distance will the directions of orientation of the planets' orbital ellipses stay constant as they are observed to do apart from small effects attributable to inter-planetary perturbations.
In regard to evidence that still survives of the earlier history, manuscripts written by Newton in the 1660s show that Newton himself had arrived by 1669 at proofs that in a circular case of planetary motion, 'endeavour to recede' (what was later called centrifugal force) had an inverse-square relation with distance from the center. After his 1679-1680 correspondence with Hooke, Newton adopted the language of inward or centripetal force. According to Newton scholar J Bruce Brackenridge, although much has been made of the change in language and difference of point of view, as between centrifugal or centripetal forces, the actual computations and proofs remained the same either way. They also involved the combination of tangential and radial displacements, which Newton was making in the 1660s. The lesson offered by Hooke to Newton here, although significant, was one of perspective and did not change the analysis. This background shows there was basis for Newton to deny deriving the inverse square law from Hooke.
Newton's acknowledgment
On the other hand, Newton did accept and acknowledge, in all editions of the 'Principia', that Hooke (but not exclusively Hooke) had separately appreciated the inverse square law in the solar system. Newton acknowledged Wren, Hooke and Halley in this connection in the Scholium to Proposition 4 in Book 1. Newton also acknowledged to Halley that his correspondence with Hooke in 1679-80 had reawakened his dormant interest in astronomical matters, but that did not mean, according to Newton, that Hooke had told Newton anything new or original: "yet am I not beholden to him for any light into that business but only for the diversion he gave me from my other studies to think on these things & for his dogmaticalness in writing as if he had found the motion in the Ellipsis, which inclined me to try it ...".)Modern controversy
Since the time of Newton and Hooke, scholarly discussion has also touched on the question of whether Hooke's 1679 mention of 'compounding the motions' provided Newton with something new and valuable, even though that was not a claim actually voiced by Hooke at the time. As described above, Newton's manuscripts of the 1660s do show him actually combining tangential motion with the effects of radially directed force or endeavour, for example in his derivation of the inverse square relation for the circular case. They also show Newton clearly expressing the concept of linear inertia—for which he was indebted to Descartes' work published 1644 (as Hooke probably was). These matters do not appear to have been learned by Newton from Hooke.Nevertheless, a number of authors have had more to say about what Newton gained from Hooke and some aspects remain controversial. The fact that most of Hooke's private papers had been destroyed or disappeared does not help to establish the truth.
Newton's role in relation to the inverse square law was not as it has sometimes been represented, he did not claim to think it up as a bare idea. What Newton did was to show how the inverse-square law of attraction had many necessary mathematical connections with observable features of the motions of bodies in the solar system; and that they were related in such a way that the observational evidence and the mathematical demonstrations, taken together, gave reason to believe that the inverse square law was not just approximately true but exactly true (to the accuracy achievable in Newton's time and for about two centuries afterwards – and with some loose ends of points that could not yet be certainly examined, where the implications of the theory had not yet been adequately identified or calculated).
In the light of the background described above, it becomes understandable how, about thirty years after Newton's death in 1727, Alexis Clairaut, a mathematical astronomer eminent in his own right in the field of gravitational studies, wrote after reviewing what Hooke published, that "One must not think that this idea ... of Hooke diminishes Newton's glory"; and that "the example of Hooke" serves "to show what a distance there is between a truth that is glimpsed and a truth that is demonstrated".
Bodies with spatial extent
If the bodies in question have spatial extent (rather than being theoretical point masses), then the gravitational force between them is calculated by summing the contributions of the notional point masses which constitute the bodies. In the limit, as the component point masses become "infinitely small", this entails integratingIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
the force (in vector form, see below) over the extents of the two bodies
Physical body
In physics, a physical body or physical object is a collection of masses, taken to be one...
.
In this way it can be shown that an object with a spherically-symmetric distribution of mass exerts the same gravitational attraction on external bodies as if all the object's mass were concentrated at a point at its centre. (This is not generally true for non-spherically-symmetrical bodies.)
For points inside a spherically-symmetric distribution of matter, Newton's Shell theorem
Shell theorem
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
can be used to find the gravitational force. The theorem tells us how different parts of the mass distribution affect the gravitational force measured at a point located a distance r0 from the center of the mass distribution:
- The portion of the mass that is located at radii r < r0 causes the same force at r0 as if all of the mass enclosed within a sphere of radius r0 was concentrated at the center of the mass distribution (as noted above).
- The portion of the mass that is located at radii r > r0 exerts no net gravitational force at the distance r0 from the center. That is, the individual gravitational forces exerted by the elements of the sphere out there, on the point at r0, cancel each other out.
As a consequence, for example, within a shell of uniform thickness and density there is no net gravitational acceleration anywhere within the hollow sphere.
Vector form
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
to account for the direction of the gravitational force as well as its magnitude. In this formula, quantities in bold represent vectors.
-
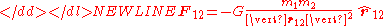
where- F12 is the force applied on object 2 due to object 1,
- G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, - m1 and m2 are respectively the masses of objects 1 and 2,
- |r12| = |r2 − r1| is the distance between objects 1 and 2, and
-
is the unit vector from object 1 to 2.
It can be seen that the vector form of the equation is the same as the scalarScalar (physics)In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
form given earlier, except that F is now a vector quantity, and the right hand side is multiplied by the appropriate unit vector. Also, it can be seen that F12 = −F21.
Gravitational field
The gravitational field is a vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
that describes the gravitational force which would be applied on an object in any given point in space, per unit mass. It is actually equal to the gravitational accelerationGravitational accelerationIn physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
at that point.
It is a generalization of the vector form, which becomes particularly useful if more than 2 objects are involved (such as a rocket between the Earth and the Moon). For 2 objects (e.g. object 2 is a rocket, object 1 the Earth), we simply write r instead of r12 and m instead of m2 and define the gravitational field g(r) as:
-
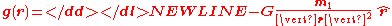
so that we can write:
This formulation is dependent on the objects causing the field. The field has units of acceleration; in SISiSi, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
, this is m/s2.
Gravitational fields are also conservative; that is, the work done by gravity from one position to another is path-independent. This has the consequence that there exists a gravitational potential field V(r) such that
If m1 is a point mass or the mass of a sphere with homogeneous mass distribution, the force field g(r) outside the sphere is isotropic, i.e., depends only on the distance r from the center of the sphere. In that case
Problems with Newton's theory
Newton's description of gravity is sufficiently accurate for many practical purposes and is therefore widely used. Deviations from it are small when the dimensionless quantities φ/c2 and (v/c)2 are both much less than one, where φ is the gravitational potential, v is the velocity of the objects being studied, and c is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
For example, Newtonian gravity provides an accurate description of the Earth/Sun system, since
-
where rorbit is the radius of the Earth's orbit around the Sun.
In situations where either dimensionless parameter is large, then
general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
must be used to describe the system. General relativity reduces to Newtonian gravity in the limit of small potential and low velocities, so Newton's law of gravitation is often said to be the low-gravity limit of general relativity.
Theoretical concerns with Newton's theory
- There is no immediate prospect of identifying the mediator of gravity. Attempts by physicists to identify the relationship between the gravitational force and other known fundamental forces are not yet resolved, although considerable headway has been made over the last 50 years (See: Theory of everythingTheory of everythingA theory of everything is a putative theory of theoretical physics that fully explains and links together all known physical phenomena, and predicts the outcome of any experiment that could be carried out in principle....
and Standard ModelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
). Newton himself felt that the concept of an inexplicable action at a distanceAction at a distance (physics)In physics, action at a distance is the interaction of two objects which are separated in space with no known mediator of the interaction. This term was used most often in the context of early theories of gravity and electromagnetism to describe how an object responds to the influence of distant...
was unsatisfactory (see "Newton's reservations" below), but that there was nothing more that he could do at the time.
- Newton's Theory of Gravitation requires that the gravitational force be transmitted instantaneously. Given the classical assumptions of the nature of space and time before the development of General Relativity, a significant propagation delay in gravity leads to unstable planetary and stellar orbits.
Observations conflicting with Newton's theory
- Newton's Theory does not fully explain the precessionPrecessionPrecession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of the perihelion of the orbitOrbitIn physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s of the planets, especially of planetPlanetA planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
MercuryMercury (planet)Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
, which was detected long after the life of Newton. There is a 43 arcsecond per century discrepancy between the Newtonian calculation, which arises only from the gravitational attractions from the other planets, and the observed precession, made with advanced telescopes during the 19th Century.
- The predicted angular deflection of light rays by gravity that is calculated by using Newton's Theory is only one-half of the deflection that is actually observed by astronomers. Calculations using General Relativity are in much closer agreement with the astronomical observations.
The observed fact that the gravitational mass and the inertial mass is the same for all objects is unexplained within Newton's Theories. General RelativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
takes this as a basic principle. See the Equivalence PrincipleEquivalence principleIn the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
. In point of fact, the experiments of Galileo GalileiGalileo GalileiGalileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
, decades before Newton, established that objects that have the same air or fluid resistance are accelerated by the force of the Earth's gravity equally, regardless of their different inertial masses. Yet, the forces and energies that are required to accelerate various masses is completely dependent upon their different inertial masses, as can be seen from Newton's Second Law of Motion, F = ma.
The problem is that Newton's Theories and his mathematical formulas explain and permit the (inaccurate) calculation of the effects of the precession of the perihelions of the orbits and the deflection of light rays. However, they did not and do not explain the equivalence of the behavior of various masses under the influence of gravity, independent of the quantities of matter involved.
Newton's reservations
While Newton was able to formulate his law of gravity in his monumental work, he was deeply uncomfortable with the notion of "action at a distance" which his equations implied. In 1692, in his third letter to Bentley, he wrote: "That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one another, is to me so great an absurdity that, I believe, no man who has in philosophic matters a competent faculty of thinking could ever fall into it."
He never, in his words, "assigned the cause of this power". In all other cases, he used the phenomenon of motion to explain the origin of various forces acting on bodies, but in the case of gravity, he was unable to experimentally identify the motion that produces the force of gravity (although he invented two mechanical hypothesesMechanical explanations of gravitationMechanical explanations of gravitation are attempts to explain the action of gravity by aid of basic mechanical processes, such as pressure forces caused by pushes, and without the use of any action at a distance. These theories were developed from the 16th until the 19th century in connection...
in 1675 and 1717). Moreover, he refused to even offer a hypothesis as to the cause of this force on grounds that to do so was contrary to sound science. He lamented that "philosophers have hitherto attempted the search of nature in vain" for the source of the gravitational force, as he was convinced "by many reasons" that there were "causes hitherto unknown" that were fundamental to all the "phenomena of nature". These fundamental phenomena are still under investigation and, though hypotheses abound, the definitive answer has yet to be found. And in Newton's 1713 General ScholiumGeneral ScholiumThe General Scholium is an essay written by Isaac Newton, appended to his work of Philosophiæ Naturalis Principia Mathematica, known as the Principia. General Scholium was first published with the second edition of the Principia and reappeared with some additions and modifications on the third ...
in the second edition of Principia: "I have not yet been able to discover the cause of these properties of gravity from phenomena and I feign no hypothesesHypotheses non fingoHypotheses non fingo is a famous phrase used by Isaac Newton in an essay General Scholium which was appended to the second edition of the Principia....
... It is enough that gravity does really exist and acts according to the laws I have explained, and that it abundantly serves to account for all the motions of celestial bodies."
Einstein's solution
These objections were rendered moot by Einstein's theory of general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, in which gravitation is an attribute of curved spacetime instead of being due to a force propagated between bodies. In Einstein's theory, masses distort spacetime in their vicinity, and other particles move in trajectories determined by the geometry of spacetime. This allowed a description of the motions of light and mass that was consistent with all available observations. In general relativity, the gravitational force is a fictitious forceFictitious forceA fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
due to the curvature of spacetime, because the gravitational accelerationGravitational accelerationIn physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
of a body in free fallFree fallFree fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...
is due to its world lineWorld lineIn physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
being a geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
of spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
.
See also
- Newton's cannonballNewton's cannonballNewton's cannonball was a thought experiment Isaac Newton used to hypothesize that the force of gravity was universal, and it was the key force for planetary motion...
- Newton's laws of motionNewton's laws of motionNewton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
- Kepler orbitKepler orbitIn celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space...
, the analysis of Newton's laws as it applies to orbits - Gauss's law for gravity
- Static forces and virtual-particle exchangeStatic forces and virtual-particle exchangeStatic force fields are fields, such as a simple electric, magnetic or gravitational fields, that exist without excitations. The most common approximation method that physicists use for scattering calculations can be interpreted as static forces arising from the interactions between two bodies...
External links
- There is no immediate prospect of identifying the mediator of gravity. Attempts by physicists to identify the relationship between the gravitational force and other known fundamental forces are not yet resolved, although considerable headway has been made over the last 50 years (See: Theory of everything
-
