Nilpotent cone
Encyclopedia
In mathematics
, the nilpotent cone
of a finite-dimensional semisimple Lie algebra 
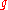is the set of elements that act nilpotently in all representations of 
In other words,
The nilpotent cone is an irreducible subvariety
of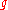
(considered as a 
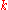-vector space
).
, the Lie algebra of 2×2 matrices
with vanishing trace
, is the variety of all 2×2 traceless matrices with rank
less than or equal to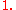
----
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the nilpotent cone
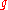of a finite-dimensional semisimple Lie algebra is the set of elements that act nilpotently in all representations of In other words,The nilpotent cone is an irreducible subvariety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
of
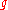(considered as a 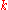-vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
).
Example
The nilpotent cone of, the Lie algebra of 2×2 matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with vanishing trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
, is the variety of all 2×2 traceless matrices with rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
less than or equal to
----
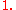