Non-Hausdorff manifold
Encyclopedia
In mathematics
, it is a usual axiom of a manifold
to be a Hausdorff space
, and this is assumed throughout geometry and topology
: "manifold" means "(second countable) Hausdorff manifold".
In general topology
, this axiom is relaxed, and one studies non-Hausdorff manifolds: spaces locally homeomorphic to Euclidean space
, but not necessarily Hausdorff.
This is the quotient space
of two copies of the real line
with the equivalence relation
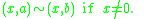
This space has a single point for each nonzero real number r and two points 0a and 0b. In this space all neighbourhoods of 0a intersect all neighbourhoods of 0b, so it is non-Hausdorff.
Further, the line with two origins does not have the homotopy type of a CW-complex, or of any Hausdorff space.
This is the quotient space
of two copies of the real line
with the equivalence relation
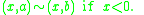
This space has a single point for each negative real number r and two points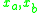
for every non-negative number: it has a "fork" at zero.
, such as the sheaf of continuous real functions over a manifold, is a manifold that is often non-Hausdorff. (The etale space is Hausdorff if it is a sheaf of functions with some sort of analytic continuation
property.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, it is a usual axiom of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
to be a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, and this is assumed throughout geometry and topology
Geometry and topology
In mathematics, geometry and topology is an umbrella term for geometry and topology, as the line between these two is often blurred, most visibly in local to global theorems in Riemannian geometry, and results like the Gauss–Bonnet theorem and Chern–Weil theory.Sharp distinctions between geometry...
: "manifold" means "(second countable) Hausdorff manifold".
In general topology
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, this axiom is relaxed, and one studies non-Hausdorff manifolds: spaces locally homeomorphic to Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, but not necessarily Hausdorff.
Line with two origins
The most familiar non-Hausdorff manifold is the line with two origins, or bug-eyed line.This is the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of two copies of the real line
- R × {a} and R × {b}
with the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
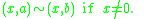
This space has a single point for each nonzero real number r and two points 0a and 0b. In this space all neighbourhoods of 0a intersect all neighbourhoods of 0b, so it is non-Hausdorff.
Further, the line with two origins does not have the homotopy type of a CW-complex, or of any Hausdorff space.
Branching line
Similar to the line with two origins is the branching line.This is the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of two copies of the real line
- R × {a} and R × {b}
with the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
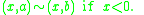
This space has a single point for each negative real number r and two points
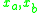for every non-negative number: it has a "fork" at zero.Etale space
The etale space of a sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
, such as the sheaf of continuous real functions over a manifold, is a manifold that is often non-Hausdorff. (The etale space is Hausdorff if it is a sheaf of functions with some sort of analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
property.)