Non-circular gear
Encyclopedia
A non-circular gear is a special gear
design with special characteristics and purpose. While a regular gear is optimized to transmit torque
to another engaged member with minimum noise and wear and with maximum efficiency
, a non-circular gear's main objective might be ratio
variations, axle displacement oscillation
s and more. Common applications include textile machines, potentiometer
s, CVTs (continuously variable transmission
s), window shade panel drives, mechanical presses and high torque hydraulic engines.
Many bicycles have an elliptical gear, see, eg., Biopace
.
A regular gear pair can be represented as two circle
s rolling together without slip. In the case of non-circular gears, those circles are replaced with anything different from a circle. For this reason NCGs in most cases are not round, but round NCGs looking like regular gears are also possible (small ratio variations result from meshing area modifications).
Generally NCG should meet all the requirements of regular gearing, but in some cases, for example variable axle
distance, could prove impossible to support and such gears require very tight manufacturing tolerances and assembling problems arise. Because of complicated geometry
, NCGs are most likely spur gears and molding
or electrical discharge machining
technology is used instead of generation.
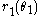be the radius of the first gear wheel as a function of angle from the axis of rotation 
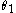, and let 
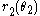be the radius of the second gear wheel as a function of angle from its axis of rotation 
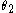. If the axles remain fixed, the distance between the axles is also fixed:
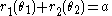
Assuming that the point of contact lies on the line connecting the axles, in order for the gears to touch without slipping, the velocity of each wheel must be equal at the point of contact and perpendicular to the line connecting the axles, which implies that:
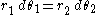
Of course, each wheel must be cyclic in its angular coordinates. If the shape of the first wheel is known, the shape of the second can often be found using the above equations. If the relationship between the angles is specified, the shapes of both wheels can often be determined analytically as well.
It is more convenient to use the circular variable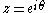
when analyzing this problem. Assuming the radius of the first gear wheel is known as a function of z, and using the relationship 
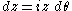, the above two equations can be combined to yield the differential equation:
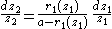
where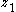
and 
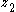describe the rotation of the first and second gears respectively. This equation can be formally solved as:
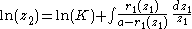
where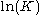
is a constant of integration.
Gear
A gear is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part in order to transmit torque. Two or more gears working in tandem are called a transmission and can produce a mechanical advantage through a gear ratio and thus may be considered a simple machine....
design with special characteristics and purpose. While a regular gear is optimized to transmit torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
to another engaged member with minimum noise and wear and with maximum efficiency
Mechanical efficiency
Mechanical efficiency measures the effectiveness of a machine in transforming the energy and power that is input to the device into an output force and movement...
, a non-circular gear's main objective might be ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
variations, axle displacement oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s and more. Common applications include textile machines, potentiometer
Potentiometer
A potentiometer , informally, a pot, is a three-terminal resistor with a sliding contact that forms an adjustable voltage divider. If only two terminals are used , it acts as a variable resistor or rheostat. Potentiometers are commonly used to control electrical devices such as volume controls on...
s, CVTs (continuously variable transmission
Continuously variable transmission
A continuously variable transmission is a transmission that can change steplessly through an infinite number of effective gear ratios between maximum and minimum values. This contrasts with other mechanical transmissions that offer a fixed number of gear ratios...
s), window shade panel drives, mechanical presses and high torque hydraulic engines.
Many bicycles have an elliptical gear, see, eg., Biopace
Biopace
Biopace is a tradename for a type of ovoid bicycle chain ring manufactured by Shimano from 1983 to 1993 The design was intended to help overcome the "dead zone" where the crank arms are vertical and riders have little mechanical advantage...
.
A regular gear pair can be represented as two circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s rolling together without slip. In the case of non-circular gears, those circles are replaced with anything different from a circle. For this reason NCGs in most cases are not round, but round NCGs looking like regular gears are also possible (small ratio variations result from meshing area modifications).
Generally NCG should meet all the requirements of regular gearing, but in some cases, for example variable axle
Axle
An axle is a central shaft for a rotating wheel or gear. On wheeled vehicles, the axle may be fixed to the wheels, rotating with them, or fixed to its surroundings, with the wheels rotating around the axle. In the former case, bearings or bushings are provided at the mounting points where the axle...
distance, could prove impossible to support and such gears require very tight manufacturing tolerances and assembling problems arise. Because of complicated geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, NCGs are most likely spur gears and molding
Molding (process)
Molding or moulding is the process of manufacturing by shaping pliable raw material using a rigid frame or model called a pattern....
or electrical discharge machining
Electrical discharge machining
Electric discharge machining , sometimes colloquially also referred to as spark machining, spark eroding, burning, die sinking or wire erosion, is a manufacturing process whereby a desired shape is obtained using electrical discharges...
technology is used instead of generation.
Mathematical description
Ignoring the gear teeth for the moment (i.e. assuming the gear teeth are very small), let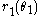 be the radius of the first gear wheel as a function of angle from the axis of rotation 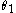, and let 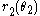be the radius of the second gear wheel as a function of angle from its axis of rotation 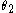. If the axles remain fixed, the distance between the axles is also fixed: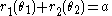Assuming that the point of contact lies on the line connecting the axles, in order for the gears to touch without slipping, the velocity of each wheel must be equal at the point of contact and perpendicular to the line connecting the axles, which implies that:
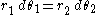
Of course, each wheel must be cyclic in its angular coordinates. If the shape of the first wheel is known, the shape of the second can often be found using the above equations. If the relationship between the angles is specified, the shapes of both wheels can often be determined analytically as well.
It is more convenient to use the circular variable
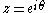when analyzing this problem. Assuming the radius of the first gear wheel is known as a function of z, and using the relationship 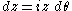, the above two equations can be combined to yield the differential equation: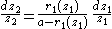where
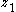and 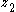describe the rotation of the first and second gears respectively. This equation can be formally solved as: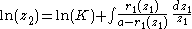where
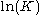is a constant of integration.Further reading
- Noncircular Gears: Design and Generation by Faydor L. Litvin, Alfonso Fuentes-Aznar, Ignacio Gonzalez-Perez, and Kenichi Hayasaka
External links
- Historic Video of Non-Circular Gears on YouTube
- The Eye of an Artist
- Kinematic Models for Design Digital Library (KMODDL)
- The Gear Oscillator
- Laczik- Involute Profile of Non-Circular Gears
- "Gear geometry and applied theory" by Faydor L. Litvin and Alfonso Fuentes
- A paper on designing of non-circular gears