Nonlinear eigenproblem
Encyclopedia
A nonlinear eigenproblem is a generalization of an ordinary eigenproblem
to equations that depend nonlinearly on the eigenvalue. Specifically, it refers to equations of the form:
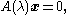
where x is a vector (the nonlinear "eigenvector") and A is a matrix
-valued function
of the number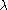
(the nonlinear "eigenvalue"). (More generally, 
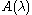could be a linear map, but most commonly it is a finite-dimensional, usually square, matrix.) A is usually required to be a holomorphic function of 
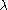(in some domain
).
For example, an ordinary linear eigenproblem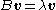
, where B is a square matrix, corresponds to 
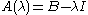, where I is the identity matrix
.
One common case is where A is a polynomial matrix
, which is called a polynomial eigenvalue problem. In particular, the specific case where the polynomial has degree
two is called a quadratic eigenvalue problem, and can be written in the form:
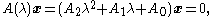
in terms of the constant square matrices A0,1,2. This can be converted into an ordinary linear generalized eigenproblem of twice the size by defining a new vector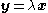
. In terms of x and y, the quadratic eigenvalue problem becomes:
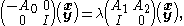
where I is the identity matrix. More generally, if A is a matrix polynomial of degree d, then one can convert the nonlinear eigenproblem into a linear (generalized) eigenproblem of d times the size.
Besides converting them to ordinary eigenproblems, which only works if A is polynomial, there are other methods of solving nonlinear eigenproblems based on the Jacobi-Davidson algorithm or based on Newton's method
(related to inverse iteration
).
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
to equations that depend nonlinearly on the eigenvalue. Specifically, it refers to equations of the form:
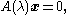
where x is a vector (the nonlinear "eigenvector") and A is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the number
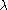(the nonlinear "eigenvalue"). (More generally, 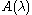could be a linear map, but most commonly it is a finite-dimensional, usually square, matrix.) A is usually required to be a holomorphic function of 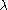(in some domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
).
For example, an ordinary linear eigenproblem
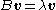, where B is a square matrix, corresponds to 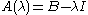, where I is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
One common case is where A is a polynomial matrix
Polynomial matrix
A polynomial matrix or sometimes matrix polynomial is a matrix whose elements are univariate or multivariate polynomials. A λ-matrix is a matrix whose elements are polynomials in λ....
, which is called a polynomial eigenvalue problem. In particular, the specific case where the polynomial has degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
two is called a quadratic eigenvalue problem, and can be written in the form:
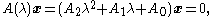
in terms of the constant square matrices A0,1,2. This can be converted into an ordinary linear generalized eigenproblem of twice the size by defining a new vector
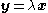. In terms of x and y, the quadratic eigenvalue problem becomes: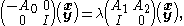where I is the identity matrix. More generally, if A is a matrix polynomial of degree d, then one can convert the nonlinear eigenproblem into a linear (generalized) eigenproblem of d times the size.
Besides converting them to ordinary eigenproblems, which only works if A is polynomial, there are other methods of solving nonlinear eigenproblems based on the Jacobi-Davidson algorithm or based on Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
(related to inverse iteration
Inverse iteration
In numerical analysis, inverse iteration is an iterative eigenvalue algorithm. It allows to find an approximateeigenvector when an approximation to a corresponding eigenvalue is already known....
).