Normalized frequency (digital signal processing)
Encyclopedia
In digital signal processing
, the normalized frequency of a periodic signal is its frequency
expressed in units of cycles (or radians) per sample
, rather than in the usual SI
units
of hertz
(cycles per second
). The cycles-per-sample frequency is computed by dividing the cycles-per-second frequency by the sampling rate
(samples per second); symbolically, the "/second" (per second) units cancel:
/ (samples/second) = cycles/sample.
.
In filter design
, a given design can be used at different sample-rates, resulting in different frequency responses. Normalization produces a distribution that is independent of the sample rate, and thus one plot is sufficient for all possible sample rates.
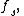in samples per second, because the frequency spectrum of a sampled signal (with real
or complex
values) is periodic with period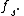
When the actual frequency
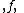has units of hertz (SI
units), the normalized frequencies, also denoted by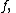
have units of cycles per sample, and the periodicity of the normalized spectrum is 1.
Alternatively, if the actual frequency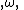
is written with units of radians per second (angular frequency
), the normalized frequencies have units of radians per sample, and the periodicity of the distribution is 2π.
If a sampled waveform is real-valued, such as a typical filter impulse response
, the periodicity of the frequency distribution is still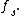
But due to symmetry, it is completely defined by the content within a span of just 
half the sampling frequency – the Nyquist frequency
. Accordingly, some filter design procedures/applications use that as the normalization reference (and the resulting units are half-cycles per sample).
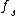= 44.1 kHz, and these 3 different choices of normalization constant
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
, the normalized frequency of a periodic signal is its frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
expressed in units of cycles (or radians) per sample
Sampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
, rather than in the usual SI
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
units
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
of hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
(cycles per second
Cycle per second
The cycle per second was a once-common unit of frequency.With the organization of the International System of Units in 1960, the cycle per second was officially replaced by the hertz, or reciprocal second—i.e. the cycle in 'cycle per second' was dropped...
). The cycles-per-sample frequency is computed by dividing the cycles-per-second frequency by the sampling rate
Sampling rate
The sampling rate, sample rate, or sampling frequency defines the number of samples per unit of time taken from a continuous signal to make a discrete signal. For time-domain signals, the unit for sampling rate is hertz , sometimes noted as Sa/s...
(samples per second); symbolically, the "/second" (per second) units cancel:
/ (samples/second) = cycles/sample.
Applications
The abstract reason for using normalized frequency is that, from the point of view of signal processing, a second is an arbitrary unit of time, while the sampling interval is a meaningful quantity (formally, a characteristic unit for the system): the frequency of a signal with respect to 1 second does not tell you about the behavior of the signal, but the frequency of a signal with respect to the sampling interval tells you the effect of sampling on the signal, via the sampling theorem. Stated alternatively, this process is called "normalization", and the sampling frequency is a normalizing constantNormalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
.
In filter design
Filter design
Filter design is the process of designing a filter , often a linear shift-invariant filter, that satisfies a set of requirements, some of which are contradictory...
, a given design can be used at different sample-rates, resulting in different frequency responses. Normalization produces a distribution that is independent of the sample rate, and thus one plot is sufficient for all possible sample rates.
Alternative normalizations
The reference value is usually the sampling frequency, denoted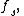 in samples per second, because the frequency spectrum of a sampled signal (with realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
values) is periodic with period
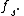When the actual frequency 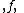has units of hertz (SISi
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units), the normalized frequencies, also denoted by
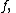have units of cycles per sample, and the periodicity of the normalized spectrum is 1.Alternatively, if the actual frequency
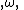is written with units of radians per second (angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
), the normalized frequencies have units of radians per sample, and the periodicity of the distribution is 2π.
If a sampled waveform is real-valued, such as a typical filter impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
, the periodicity of the frequency distribution is still
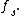But due to symmetry, it is completely defined by the content within a span of just half the sampling frequency – the Nyquist frequencyNyquist frequency
The Nyquist frequency, named after the Swedish-American engineer Harry Nyquist or the Nyquist–Shannon sampling theorem, is half the sampling frequency of a discrete signal processing system...
. Accordingly, some filter design procedures/applications use that as the normalization reference (and the resulting units are half-cycles per sample).
Example
The following table shows examples of normalized frequencies for a 1 kHz signal, a sample rate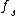 = 44.1 kHz, and these 3 different choices of normalization constant| Type | Computation | Value |
| Radians/sample | 2 π 1000 / 44100 | 0.1425 |
| cycles/sample (w.r.t. fs, sampling frequency) |
1000 / 44100 | 0.02268 |
| half-cycles/sample (w.r.t. fs/2, Nyquist frequency Nyquist frequency The Nyquist frequency, named after the Swedish-American engineer Harry Nyquist or the Nyquist–Shannon sampling theorem, is half the sampling frequency of a discrete signal processing system... ) |
1000 / 22050 | 0.04535 |