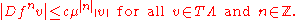Normally hyperbolic invariant manifold
Encyclopedia
A normally hyperbolic invariant manifold (NHIM) is a natural generalization of a hyperbolic fixed point and a hyperbolic set
. The difference can be described heuristically as follows: For a manifold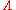 to be normally hyperbolic we are allowed to assume that the dynamics of
to be normally hyperbolic we are allowed to assume that the dynamics of 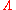 itself is neutral compared with the dynamics nearby, which is not allowed for a hyperbolic set. NHIMs were introduced by Neil Fenichel in 1972. In this and subsequent papers, Fenichel proves that NHIMs possess stable and unstable manifolds and more importantly, NHIMs and their stable and unstable manifolds persist under small perturbations. Thus, in problems involving perturbation theory, invariant manifolds exist with certain hyperbolicity properties, which can in turn be used to obtain qualitative information about a dynamical system.
itself is neutral compared with the dynamics nearby, which is not allowed for a hyperbolic set. NHIMs were introduced by Neil Fenichel in 1972. In this and subsequent papers, Fenichel proves that NHIMs possess stable and unstable manifolds and more importantly, NHIMs and their stable and unstable manifolds persist under small perturbations. Thus, in problems involving perturbation theory, invariant manifolds exist with certain hyperbolicity properties, which can in turn be used to obtain qualitative information about a dynamical system.
smooth manifold, f: M → M a diffeomorphism
, and Df: TM → TM the differential of f. An f-invariant submanifold
Λ of M is said to be a normally hyperbolic invariant manifold if the restriction to Λ of the tangent bundle of M admits a splitting into a sum of three Df-invariant subbundles, one being the tangent bundle of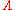 , the others being the stable bundle and the unstable bundle and denoted Es and Eu, respectively. With respect to some Riemannian metric on M, the restriction of Df to Es must be a contraction and the restriction of Df to Eu must be an expansion, and must be relatively neutral on
, the others being the stable bundle and the unstable bundle and denoted Es and Eu, respectively. With respect to some Riemannian metric on M, the restriction of Df to Es must be a contraction and the restriction of Df to Eu must be an expansion, and must be relatively neutral on  . Thus, there exist constants
. Thus, there exist constants 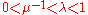 and c > 0 such that
and c > 0 such that
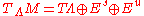

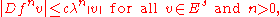
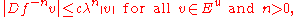
and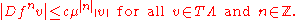
Hyperbolic set
In dynamical systems theory, a subset Λ of a smooth manifold M is said to have a hyperbolic structure with respect to a smooth map f if its tangent bundle may be split into two invariant subbundles, one of which is contracting and the other is expanding under f, with respect to some...
. The difference can be described heuristically as follows: For a manifold
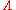 to be normally hyperbolic we are allowed to assume that the dynamics of
to be normally hyperbolic we are allowed to assume that the dynamics of 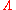 itself is neutral compared with the dynamics nearby, which is not allowed for a hyperbolic set. NHIMs were introduced by Neil Fenichel in 1972. In this and subsequent papers, Fenichel proves that NHIMs possess stable and unstable manifolds and more importantly, NHIMs and their stable and unstable manifolds persist under small perturbations. Thus, in problems involving perturbation theory, invariant manifolds exist with certain hyperbolicity properties, which can in turn be used to obtain qualitative information about a dynamical system.
itself is neutral compared with the dynamics nearby, which is not allowed for a hyperbolic set. NHIMs were introduced by Neil Fenichel in 1972. In this and subsequent papers, Fenichel proves that NHIMs possess stable and unstable manifolds and more importantly, NHIMs and their stable and unstable manifolds persist under small perturbations. Thus, in problems involving perturbation theory, invariant manifolds exist with certain hyperbolicity properties, which can in turn be used to obtain qualitative information about a dynamical system. Definition
Let M be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
smooth manifold, f: M → M a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
, and Df: TM → TM the differential of f. An f-invariant submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
Λ of M is said to be a normally hyperbolic invariant manifold if the restriction to Λ of the tangent bundle of M admits a splitting into a sum of three Df-invariant subbundles, one being the tangent bundle of
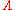 , the others being the stable bundle and the unstable bundle and denoted Es and Eu, respectively. With respect to some Riemannian metric on M, the restriction of Df to Es must be a contraction and the restriction of Df to Eu must be an expansion, and must be relatively neutral on
, the others being the stable bundle and the unstable bundle and denoted Es and Eu, respectively. With respect to some Riemannian metric on M, the restriction of Df to Es must be a contraction and the restriction of Df to Eu must be an expansion, and must be relatively neutral on  . Thus, there exist constants
. Thus, there exist constants 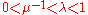 and c > 0 such that
and c > 0 such that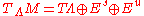

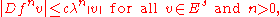
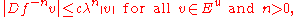
and