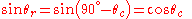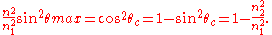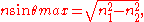Numerical aperture
Encyclopedia
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one material to another provided there is no optical power
Optical power
Optical power is the degree to which a lens, mirror, or other optical system converges or diverges light. It is equal to the reciprocal of the focal length of the device. The dioptre is the most common unit of measurement of optical power...
at the interface. The exact definition of the term varies slightly between different areas of optics.
General optics
In most areas of optics, and especially in microscopyMicroscopy
Microscopy is the technical field of using microscopes to view samples and objects that cannot be seen with the unaided eye...
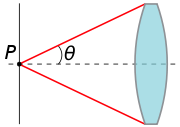
, the numerical aperture of an optical system such as an objective lens is defined by
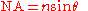
where n is the index of refraction
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
of the medium in which the lens is working (1.0 for air, 1.33 for pure water
Water
Water is a chemical substance with the chemical formula H2O. A water molecule contains one oxygen and two hydrogen atoms connected by covalent bonds. Water is a liquid at ambient conditions, but it often co-exists on Earth with its solid state, ice, and gaseous state . Water also exists in a...
, and up to 1.56 for oil
Oil
An oil is any substance that is liquid at ambient temperatures and does not mix with water but may mix with other oils and organic solvents. This general definition includes vegetable oils, volatile essential oils, petrochemical oils, and synthetic oils....
s; see also list of refractive indices), and θ is the half-angle of the maximum cone of light that can enter or exit the lens. In general, this is the angle of the real marginal ray in the system. Because the index of refraction is included, the NA of a pencil of rays is an invariant as a pencil of rays passes from one material to another through a flat surface. This is easily shown by rearranging Snell's law
Snell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
to find that
is constant across an interface.In air, the angular aperture
Angular aperture
The angular aperture of a lens is the apparent angle of the lens aperture as seen from the focal point:a = 2 \arctan \leftwheref is the focal lengthD is the diameter of the aperture.- Relation to numerical aperture :...
of the lens is approximately twice this value (within the paraxial approximation
Paraxial approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
). The NA is generally measured with respect to a particular object or image point and will vary as that point is moved. In microscopy, NA generally refers to object-space NA unless otherwise noted.
In microscopy, NA is important because it indicates the resolving power
Angular resolution
Angular resolution, or spatial resolution, describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object...
of a lens. The size of the finest detail that can be resolved is proportional to λ/2NA, where λ is the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of the light. A lens with a larger numerical aperture will be able to visualize finer details than a lens with a smaller numerical aperture. Assuming quality (diffraction limited) optics, lenses with larger numerical apertures collect more light and will generally provide a brighter image, but will provide shallower depth of field
Depth of field
In optics, particularly as it relates to film and photography, depth of field is the distance between the nearest and farthest objects in a scene that appear acceptably sharp in an image...
.
Numerical aperture is used to define the "pit size" in optical disc
Optical disc
In computing and optical disc recording technologies, an optical disc is a flat, usually circular disc which encodes binary data in the form of pits and lands on a special material on one of its flat surfaces...
formats.
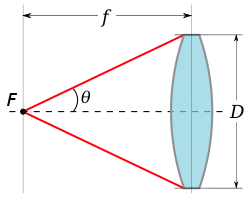
Numerical aperture versus f-number
Photography
Photography is the art, science and practice of creating durable images by recording light or other electromagnetic radiation, either electronically by means of an image sensor or chemically by means of a light-sensitive material such as photographic film...
. Instead, the angular aperture of a lens
Photographic lens
A camera lens is an optical lens or assembly of lenses used in conjunction with a camera body and mechanism to make images of objects either on photographic film or on other media capable of storing an image chemically or electronically.While in principle a simple convex lens will suffice, in...
(or an imaging mirror) is expressed by the f-number
F-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
, written or
, which is defined as the ratio of the focal lengthFocal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
to the diameter of the entrance pupil
Entrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the front of the lens system. The corresponding image of the aperture as seen through the back of the lens system is called the exit pupil...
:
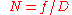
This ratio is related to the image-space numerical aperture when the lens is focused at infinity. Based on the diagram at the right, the image-space numerical aperture of the lens is:
- thus
, assuming normal use in air (
).
The approximation holds when the numerical aperture is small, and it is nearly exact even at large numerical apertures for well-corrected camera lenses. For numerical apertures less than about 0.5 (f-numbers greater than about 1) the divergence between the approximation and the full expression is less than 10%. Beyond this, the approximation breaks down. As Rudolf Kingslake explains, "It is a common error to suppose that the ratio [
] is actually equal to 
, and not 
... The tangent would, of course, be correct if the principal planes were really plane. However, the complete theory of the Abbe sine conditionAbbe sine condition
The Abbe sine condition is a condition that must be fulfilled by a lens or other optical system in order for it to produce sharp images of off-axis as well as on-axis objects...
shows that if a lens is corrected for coma and spherical aberration, as all good photographic objectives must be, the second principal plane becomes a portion of a sphere of radius f centered about the focal point, ..." In this sense, the traditional thin-lens definition and illustration of f-number is misleading, and defining it in terms of numerical aperture may be more meaningful.
"Working" or "effective" f-number
The f-number describes the light-gathering ability of the lens in the case where the marginal rays on the object side are parallel to the axis of the lens. This case is commonly encountered in photography, where objects being photographed are often far from the camera. When the object is not distant from the lens, however, the image is no longer formed in the lens's focal plane, and the f-number no longer accurately describes the light-gathering ability of the lens or the image-side numerical aperture. In this case, the numerical aperture is related to what is sometimes called the "working f-number" or "effective f-number." The working f-number is defined by modifying the relation above, taking into account the magnification from object to image: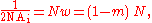
where
is the working f-number, 
is the lens's magnificationMagnification
Magnification is the process of enlarging something only in appearance, not in physical size. This enlargement is quantified by a calculated number also called "magnification"...
for an object a particular distance away, and the NA is defined in terms of the angle of the marginal ray as before. The magnification here is typically negative; in photography, the factor is sometimes written as 1 + m, where m represents the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the magnification; in either case, the correction factor is 1 or greater.
The two equalities in the equation above are each taken by various authors as the definition of working f-number, as the cited sources illustrate. They are not necessarily both exact, but are often treated as if they are. The actual situation is more complicated — as Allen R. Greenleaf explains, "Illuminance varies inversely as the square of the distance between the exit pupil of the lens and the position of the plate or film. Because the position of the exit pupil usually is unknown to the user of a lens, the rear conjugate focal distance is used instead; the resultant theoretical error so introduced is insignificant with most types of photographic lenses."
Conversely, the object-side numerical aperture is related to the f-number by way of the magnification (tending to zero for a distant object):
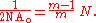
Laser physics
In laser physicsLaser Physics
Laser Physics is an international scientific journal published by Nauka/Interperiodica. It is distributed through the Springer.-Topics covered:The journal specializes in laser physics, but also publishes papers about:...
, the numerical aperture is defined slightly differently. Laser beams spread out as they propagate, but slowly. Far away from the narrowest part of the beam, the spread is roughly linear with distance—the laser beam forms a cone of light in the "far field". The relation used to define the NA of the laser beam is the same as that used for an optical system,
but θ is defined differently. Laser beams typically do not have sharp edges like the cone of light that passes through the aperture
Aperture
In optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture of an optical system is the opening that determines the cone angle of a bundle of rays that come to a focus in the image plane. The aperture determines how collimated the admitted rays are,...
of a lens does. Instead, the irradiance
Irradiance
Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter...
falls off gradually away from the center of the beam. It is very common for the beam to have a Gaussian
Gaussian beam
In optics, a Gaussian beam is a beam of electromagnetic radiation whose transverse electric field and intensity distributions are well approximated by Gaussian functions. Many lasers emit beams that approximate a Gaussian profile, in which case the laser is said to be operating on the fundamental...
profile. Laser physicists typically choose to make θ the divergence of the beam: the far-field angle between the propagation direction and the distance from the beam axis for which the irradiance drops to 1/e2 times the wavefront total irradiance. The NA of a Gaussian laser beam is then related to its minimum spot size by
where λ0 is the vacuum wavelength of the light, and 2w0 is the diameter of the beam at its narrowest spot, measured between the 1/e2 irradiance points ("Full width at e−2 maximum of the intensity"). Note that this means that a laser beam that is focused to a small spot will spread out quickly as it moves away from the focus, while a large-diameter laser beam can stay roughly the same size over a very long distance.
Fiber optics
A multi-mode optical fiberMulti-mode optical fiber
Multi-mode optical fiber is a type of optical fiber mostly used for communication over short distances, such as within a building or on a campus...
will only propagate light that enters the fiber within a certain cone, known as the acceptance cone of the fiber. The half-angle of this cone is called the acceptance angle, θmax. For step-index
Step-index profile
For an optical fiber, a step-index profile is a refractive index profile characterized by a uniform refractive index within the core and a sharp decrease in refractive index at the core-cladding interface so that the cladding is of a lower refractive index. The step-index profile corresponds to a...
multimode fiber, the acceptance angle is determined only by the indices of refraction:
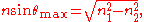
where n1 is the refractive index of the fiber core, and n2 is the refractive index of the cladding
Cladding (fiber optics)
Cladding is one or more layers of material of lower refractive index, in intimate contact with a core material of higher refractive index. The cladding causes light to be confined to the core of the fiber by total internal reflection at the boundary between the two. Light propagation in the...
.
When a light ray is incident from a medium of refractive index
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
n to the core of index n1 at the maximum acceptance angle, Snell's law
Snell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
at the medium–core interface gives
From the geometry of the above figure we have:
where
is the critical angle for total internal reflectionTotal internal reflection
Total internal reflection is an optical phenomenon that happens when a ray of light strikes a medium boundary at an angle larger than a particular critical angle with respect to the normal to the surface. If the refractive index is lower on the other side of the boundary and the incident angle is...
.
Substituting cos θc for sin θr in Snell's law we get:
By squaring both sides
Solving, we find the formula stated above:
This has the same form as the numerical aperture in other optical systems, so it has become common to define the NA of any type of fiber to be
where n1 is the refractive index along the central axis of the fiber. Note that when this definition is used, the connection between the NA and the acceptance angle of the fiber becomes only an approximation. In particular, manufacturers often quote "NA" for single-mode fiber based on this formula, even though the acceptance angle for single-mode fiber is quite different and cannot be determined from the indices of refraction alone.
The number of bound modes
Transverse mode
A transverse mode of a beam of electromagnetic radiation is a particular electromagnetic field pattern of radiation measured in a plane perpendicular to the propagation direction of the beam...
, the mode volume, is related to the normalized frequency and thus to the NA.
In multimode fibers, the term equilibrium numerical aperture is sometimes used. This refers to the numerical aperture with respect to the extreme exit angle of a ray
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
emerging from a fiber in which equilibrium mode distribution
Equilibrium mode distribution
The equilibrium mode [power] distribution of light travelling in an optical waveguide or fiber, is the distribution of light that is no longer changing with fibre length or with input modal excitation. This phenomenon requires both mode filtering and mode mixing to occur in the fibre to produce a...
has been established.
External links
- "Microscope Objectives: Numerical Aperture and Resolution" by Mortimer Abramowitz and Michael W. Davidson, Molecular Expressions: Optical Microscopy Primer (website), Florida State UniversityFlorida State UniversityThe Florida State University is a space-grant and sea-grant public university located in Tallahassee, Florida, United States. It is a comprehensive doctoral research university with medical programs and significant research activity as determined by the Carnegie Foundation...
, April 22, 2004. - "Basic Concepts and Formulas in Microscopy: Numerical Aperture" by Michael W. Davidson, NikonNikon, also known as just Nikon, is a multinational corporation headquartered in Tokyo, Japan, specializing in optics and imaging. Its products include cameras, binoculars, microscopes, measurement instruments, and the steppers used in the photolithography steps of semiconductor fabrication, of which...
MicroscopyU (website). - "Numerical aperture", Encyclopedia of Laser Physics and Technology (website).
- "Numerical Aperture and Resolution", UCLA Brain Research Institute Microscopy Core Facilities (website), 2007.