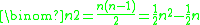In mathematics

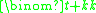Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a numerical polynomial is a polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

 with rational

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

 coefficients that takes integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

 values on integers. They are also called integer-valued polynomials.

They are objects of study in their own right in algebra, and are frequently used in algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

.

Classification

Polynomials with integer coefficients are numerical polynomials, but they are not the only ones. Binomial coefficients, thought of as rational polynomials, are also numerical polynomials.
For instance,

is numerical but does not have integer coefficients.

In fact, binomial coefficients generate numerical polynomials: every numerical polynomial is a unique integer linear combination of binomial coefficients, via the discrete Taylor series: binomial coefficients are numerical polynomials, and conversely, the discrete difference of an integer series is an integer series, so the discrete Taylor series of an integer series generated by a polynomial has integer coefficients (and is a finite series).

See binomial coefficient#Binomial coefficients as a basis for the space of polynomials for more information.

Other rings

Numerical polynomials can be defined over other rings and fields, in which case the integer-valued polynomials above are referred to as classical numerical polynomials.

Applications

The K-theory

Topological K-theory

In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...

 of BU(n)

Classifying space for U(n)

In mathematics, the classifying space for the unitary group U is a space B together with a universal bundle E such that any hermitian bundle on a paracompact space X is the pull-back of E by a map X → B unique up to homotopy.This space with its universal fibration may be constructed as either# the...

 is numerical (symmetric) polynomials.

The Hilbert polynomial

Hilbert polynomial

In commutative algebra, the Hilbert polynomial of a graded commutative algebra or graded module is a polynomial in one variable that measures the rate of growth of the dimensions of its homogeneous components...

of a polynomial ring in k + 1 variables is the numerical polynomial .
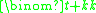