
Néron model
Encyclopedia
In algebraic geometry
, a Néron model (or Néron minimal model, or minimal model)
for an abelian variety
AK defined over a local field
K is the "best possible" group scheme AO defined over the ring of integers R of the local field K that becomes isomorphic to AK after base change from R to K.
They were introduced by André Néron
(1964).
with field of fractions K, and suppose that AK is an abelian variety over K. Then a Néron model is defined to be a universal separated smooth scheme AR over R with a rational map to AK.
More precisely, this means that AR is a separated smooth scheme over R with general fiber AK, such that any rational map from
a smooth scheme over R to AR can be extended to a unique morphism (Néron mapping property). In particular, the canonical map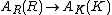 is a group isomorphism.
is a group isomorphism.
Néron models exist and are unique (up to unique isomorphism) and are commutative quasi-projective group scheme
s over R. The fiber of a Néron model over a closed point of Spec(R) is a smooth commutative algebraic group
, but needs not be an abelian variety: for example, it may be disconnected, or unipotent, or a torus. Néron models exist as well for certain commutative groups other than abelian varieties, e.g., tori, but these are only locally of finite type. Néron models does not exist for the additive group.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a Néron model (or Néron minimal model, or minimal model)
for an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
AK defined over a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
K is the "best possible" group scheme AO defined over the ring of integers R of the local field K that becomes isomorphic to AK after base change from R to K.
They were introduced by André Néron
André Néron
André Néron was a French mathematician at the Université de Poitiers who worked on elliptic curves and Abelian varieties...
(1964).
Definition
Suppose that R is a Dedekind domainDedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
with field of fractions K, and suppose that AK is an abelian variety over K. Then a Néron model is defined to be a universal separated smooth scheme AR over R with a rational map to AK.
More precisely, this means that AR is a separated smooth scheme over R with general fiber AK, such that any rational map from
a smooth scheme over R to AR can be extended to a unique morphism (Néron mapping property). In particular, the canonical map
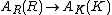 is a group isomorphism.
is a group isomorphism.Néron models exist and are unique (up to unique isomorphism) and are commutative quasi-projective group scheme
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
s over R. The fiber of a Néron model over a closed point of Spec(R) is a smooth commutative algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
, but needs not be an abelian variety: for example, it may be disconnected, or unipotent, or a torus. Néron models exist as well for certain commutative groups other than abelian varieties, e.g., tori, but these are only locally of finite type. Néron models does not exist for the additive group.
Properties
- The formation of Néron models commutes with products.
- The formation of Néron models commutes with étale base change.
- An Abelian scheme A/S is the Néron model of its generic fibre.

