
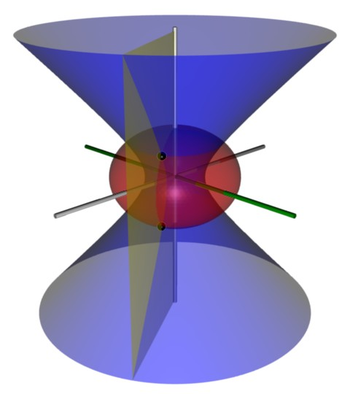
Oblate spheroidal coordinates
Encyclopedia

Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
that results from rotating the two-dimensional elliptic coordinate system
Elliptic coordinates
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in whichthe coordinate lines are confocal ellipses and hyperbolae...
about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius
 in the x-y plane. (Rotation about the other axis produces the prolate spheroidal coordinates
in the x-y plane. (Rotation about the other axis produces the prolate spheroidal coordinatesProlate spheroidal coordinates
Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating a spheroid around its major axis, i.e., the axis on which the foci are located...
.) Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates
Ellipsoidal coordinates
Ellipsoidal coordinates are a three-dimensional orthogonal coordinate system that generalizes the two-dimensional elliptic coordinate system...
in which the two largest semi-axes are equal in length.
Oblate spheroidal coordinates are often useful in solving partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s when the boundary conditions are defined on an oblate spheroid or a hyperboloid of revolution. For example, they played an important role in the calculation of the Perrin friction factors
Perrin friction factors
In hydrodynamics, the Perrin friction factors are multiplicative adjustments to the translational and rotational friction of a rigid spheroid, relative to the corresponding frictions in spheres of the same volume...
, which contributed to the awarding of the 1926 Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
to Jean Baptiste Perrin
Jean Baptiste Perrin
Jean Baptiste Perrin was a French physicist and Nobel laureate.-Early years:Born in Lille, France, Perrin attended the École Normale Supérieure, the elite grande école in Paris. He became an assistant at the school during the period of 1894-97 when he began the study of cathode rays and X-rays...
. These friction factors determine the rotational diffusion
Rotational diffusion
Rotational diffusion is a process by which the equilibrium statistical distribution of the overall orientation of particles or molecules is maintained or restored...
of molecules, which affects the feasibility of many techniques such as protein NMR and from which the hydrodynamic volume and shape of molecules can be inferred. Oblate spheroidal coordinates are also useful in problems of electromagnetism (e.g., dielectric constant of charged oblate molecules), acoustics (e.g., scattering of sound through a circular hole), fluid dynamics (e.g., the flow of water through a firehose nozzle) and the diffusion of materials and heat (e.g., cooling of a red-hot coin in a water bath).
Definition (μ, ν, φ)
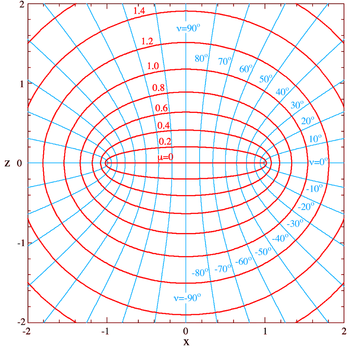

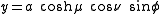
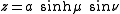
where μ is a nonnegative real number and the angle ν lies between ±90°. The azimuthal angle φ can fall anywhere on a full circle, between ±180°. These coordinates are favored over the alternatives below because they are not degenerate; every point in Cartesian coordinates (x, y, z) is described by exactly one set of coordinates (μ, ν, φ), and vice versa.
Coordinate surfaces
The surfaces of constant μ form oblate spheroids, by the trigonometric identity
since they are ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s rotated about the z-axis, which separates their foci. An ellipse in the x-z plane (Figure 2) has a major semiaxis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of length a cosh μ along the x-axis, whereas its minor semiaxis
Semi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
has length a sinh μ along the z-axis. The foci of all the ellipses in the x-z plane are located on the x-axis at ±a.
Similarly, the surfaces of constant ν form one-sheet half hyperboloids of revolution by the hyperbolic trigonometric identity

For positive ν, the half-hyperboloid is above the x-y plane (i.e., has positive z) whereas for negative ν, the half-hyperboloid is below the x-y plane (i.e., has negative z). Geometrically, the angle ν corresponds to the angle of the asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
s of the hyperbola. The foci of all the hyperbolae are likewise located on the x-axis at ±a.
Inverse transformation
The (μ, ν, φ) coordinates may be calculated from the Cartesian coordinates (x, y, z) as follows. The azimuthal angle φ is given by the formula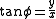
The cylindrical radius ρ of the point P is given by
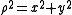
and its distances to the foci in the plane defined by φ is given by

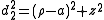
The remaining coordinates μ and ν can be calculated from the equations
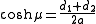
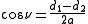
where the sign of μ is always non-negative, and the sign of ν is the same as that of z.
Scale factors
The scale factors for the coordinates μ and ν are equal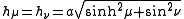
whereas the azimuthal scale factor equals
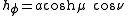
Consequently, an infinitesimal volume element equals
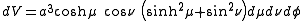
and the Laplacian can be written
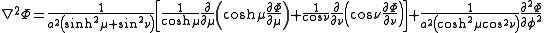
Other differential operators such as
 and
and  can be expressed in the coordinates (μ, ν, φ) by substituting the scale factors into the general formulae found in orthogonal coordinates
can be expressed in the coordinates (μ, ν, φ) by substituting the scale factors into the general formulae found in orthogonal coordinatesOrthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
Definition (ζ, ξ, φ)
Another set of oblate spheroidal coordinates are sometimes used where
are sometimes used where 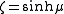 and
and 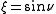 (Smythe 1968). The curves of constant
(Smythe 1968). The curves of constant 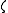 are oblate spheroids and the curves of constant
are oblate spheroids and the curves of constant 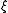 are the hyperboloids of revolution. The coordinate
are the hyperboloids of revolution. The coordinate  is restricted by
is restricted by 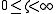 and
and  is restricted by
is restricted by 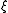 .
.The relationship to Cartesian coordinates is

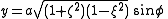
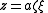
Scale factors
The scale factors for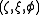 are:
are: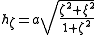
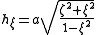
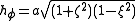
Knowing the scale factors, various functions of the coordinates can be calculated by the general method outlined in the orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
article. The infinitesimal volume element is:
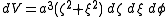
The gradient is:
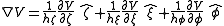
The divergence is:
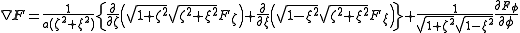
and the Laplacian equals
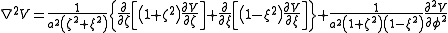
Oblate spheroidal harmonics
As is the case with spherical coordinates and spherical harmonicsSpherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
, Laplace's equation may be solved by the method of separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
to yield solutions in the form of oblate spheroidal harmonics, which are convenient to use when boundary conditions are defined on a surface with a constant oblate spheroidal coordinate.
Following the technique of separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
, a solution to Laplace's equation is written:
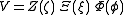
This yields three separate differential equations in each of the variables:
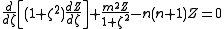
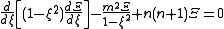
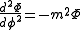
where m is a constant which is an integer because the φ variable is periodic with period 2π. n will then be an integer. The solution to these equations are:

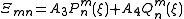
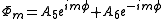
where the
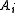 are constants and
are constants and  and
and 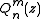 are associated Legendre polynomials of the first and second kind respectively. The product of the three solutions is called an oblate spheroidal harmonic and the general solution to Laplace's equation is written:
are associated Legendre polynomials of the first and second kind respectively. The product of the three solutions is called an oblate spheroidal harmonic and the general solution to Laplace's equation is written:
The constants will combine to yield only four independent constants for each harmonic.
Definition (σ, τ, φ)
Cosh
Cosh may refer to:* Hyperbolic cosine, a mathematical function with notation cosh* A blunt metal stick used as a weapon, also known as a blackjack...
μ and τ = cos ν. Therefore, the coordinate σ must be greater than or equal to one, whereas τ must lie between ±1, inclusive. The surfaces of constant σ are oblate spheroids, as were those of constant μ, whereas the curves of constant τ are full hyperboloids of revolution, including the half-hyperboloids corresponding to ±ν. Thus, these coordinates are degenerate; two points in Cartesian coordinates (x, y, ±z) map to one set of coordinates (σ, τ, φ). This two-fold degeneracy in the sign of z is evident from the equations transforming from oblate spheroidal coordinates to the Cartesian coordinates
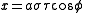
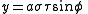
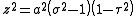
The coordinates
 and
and  have a simple relation to the distances to the focal ring. For any point, the sum
have a simple relation to the distances to the focal ring. For any point, the sum 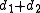 of its distances to the focal ring equals
of its distances to the focal ring equals  , whereas their difference
, whereas their difference 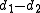 equals
equals 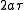 . Thus, the "far" distance to the focal ring is
. Thus, the "far" distance to the focal ring is  , whereas the "near" distance is
, whereas the "near" distance is 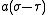 .
.Coordinate surfaces
Similar to its counterpart μ, the surfaces of constant σ form oblate spheroids
Similarly, the surfaces of constant τ form full one-sheet hyperboloids of revolution

Scale factors
The scale factors for the alternative oblate spheroidal coordinates are
are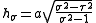
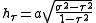
whereas the azimuthal scale factor is
 .
.Hence, the infinitesimal volume element can be written
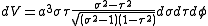
and the Laplacian equals
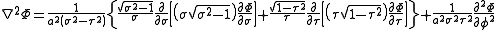
Other differential operators such as
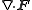 and
and 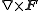 can be expressed in the coordinates
can be expressed in the coordinates  by substituting the scale factors into the general formulae found in orthogonal coordinates
by substituting the scale factors into the general formulae found in orthogonal coordinatesOrthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
As is the case with spherical coordinates, Laplaces equation may be solved by the method of separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
to yield solutions in the form of oblate spheroidal harmonics, which are convenient to use when boundary conditions are defined on a surface with a constant oblate spheroidal coordinate (See Smythe, 1968).
No angles convention
Uses ξ1 = a sinh μ, ξ2 = sin ν, and ξ3 = cos φ. Same as Morse & Feshbach (1953), substituting uk for ξk. | page = 98}} Uses hybrid coordinates ξ = sinh μ, η = sin ν, and φ.Angle convention
| page = 177}} Korn and Korn use the (μ, ν, φ) coordinates, but also introduce the degenerate (σ, τ, φ) coordinates.| page = 182 }} Like Korn and Korn (1961), but uses colatitudeColatitude
In spherical coordinates, colatitude is the complementary angle of the latitude, i.e. the difference between 90° and the latitude.-Astronomical use:The colatitude is useful in astronomy because it refers to the zenith distance of the celestial poles...
θ = 90° - ν instead of latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
ν. Moon and Spencer use the colatitude convention θ = 90° - ν, and re-name φ as ψ.
Unusual convention
Treats the oblate spheroidal coordinates as a limiting case of the general ellipsoidal coordinatesEllipsoidal coordinates
Ellipsoidal coordinates are a three-dimensional orthogonal coordinate system that generalizes the two-dimensional elliptic coordinate system...
. Uses (ξ, η, ζ) coordinates that have the units of distance squared.

