Observed information
Encyclopedia
In statistics
, the observed information, or observed Fisher information, is the negative of the second derivative (the Hessian matrix
) of the "log-likelihood" (the logarithm of the likelihood function
). It is a sample-based version of the Fisher information
.
s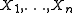
, independent and identically distributed with density f(X; θ), where θ is a (possibly unknown) vector. Then the log-likelihood of the parameters 
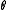given the data 
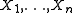is
.
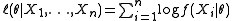We define the observed information matrix at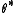
as
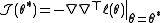
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the observed information, or observed Fisher information, is the negative of the second derivative (the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
) of the "log-likelihood" (the logarithm of the likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
). It is a sample-based version of the Fisher information
Fisher information
In mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
.
Definition
Suppose we observe random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s
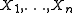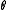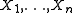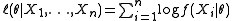, independent and identically distributed with density f(X; θ), where θ is a (possibly unknown) vector. Then the log-likelihood of the parameters given the data is.We define the observed information matrix at
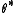as-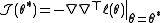
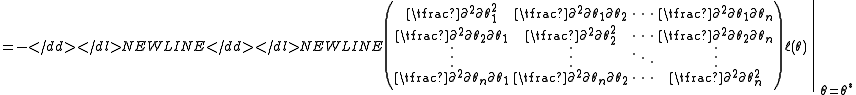
In many instances, the observed information is evaluated at the maximum-likelihood estimateMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
.
Fisher information
The Fisher informationFisher informationIn mathematical statistics and information theory, the Fisher information is the variance of the score. In Bayesian statistics, the asymptotic distribution of the posterior mode depends on the Fisher information and not on the prior...
is the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the observed information:
.
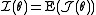Applications
In a notable article, Bradley EfronBradley EfronBradley Efron is an American statistician best known for proposing the bootstrap resampling technique, which has had a major impact in the field of statistics and virtually every area of statistical application...
and David V. HinkleyDavid V. HinkleyDavid V. Hinkley is a statistician known for his research in statistical models and inference and for his graduate-level books.-Research and graduate textbooks:He earned a PhD from the Imperial College London under the supervision of David R. Cox...
argued that the observed information should be used in preference to the expected information when employing normal approximations for the distribution of maximum-likelihood estimateMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
s.