Odds algorithm
Encyclopedia
The odds-algorithm is a mathematical method for computing optimal
strategies for a class of problems that belong to the domain of optimal stopping
problems. Their solution follows from the odds-strategy, and the importance of the
odds-strategy lies in its optimality, as explained below.
The odds-algorithm applies to a class of problems called last-success-problems. Formally, the objective in these problems is to maximize the probability of identifying in a
sequence of sequentially observed independent events the last event satisfying a specific criterion (a "specific event"). This identification must be done at the time of observation. No revisiting of preceding observations is permitted. Usually, a specific
event is defined by the decision maker as an event that is of true interest in the view of "stopping" to take a well-defined action. Such problems are encountered in several situations.
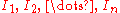with values 1 or 0. Here 
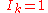stands for
the event that the kth observation is interesting (as defined by the decision maker), and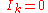
for non-interesting.
Let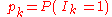
be the probability that the kth event is interesting. Further let
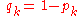and 
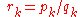. Note that
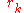represents the odds
of the kth event turning out to be interesting,
explaining the name of the odds-algorithm.
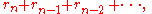
until this sum reaches or exceeds the value 1 for the first time. If this happens at index s, it saves s and the corresponding sum
If the sum of the odds does not reach 1, it sets s = 1. At the same time it computes
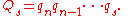
The output is
on the first interesting event from index s onwards (if any), where s is the stopping threshold of output a).
The importance of the odds-strategy, and hence of the odds-algorithm, lies in the following odds-theorem.
exist for all sequences, so that the odds-algorithm is, at the same time, optimal as an algorithm.
s over sales problems, secretary problems, portfolio
selection, (one-way) search strategies, trajectory problems and the parking problem to problems in on-line maintenance and others.
There exists, in the same spirit, an Odds-Theorem for continuous-time arrival processes with independent increments such as the Poisson process
(Bruss (2000)). In some cases, the odds are not necessarily known in advance (as in Example 2 above) so that the application of the odds-algorithm is not directly possible. In this case each step can use sequential estimates of the odds. This is meaningful, if the number of unknown parameters is not large compared with the number n of observations. The question of optimality is then more complicated, however, and requires additional studies. Generalizations of the odds-algorithm allow for different rewards for failing to stop
and wrong stops as well as replacing independence assumptions by weaker ones (Ferguson (2008)).
strategies for a class of problems that belong to the domain of optimal stopping
Optimal stopping
In mathematics, the theory of optimal stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance...
problems. Their solution follows from the odds-strategy, and the importance of the
odds-strategy lies in its optimality, as explained below.
The odds-algorithm applies to a class of problems called last-success-problems. Formally, the objective in these problems is to maximize the probability of identifying in a
sequence of sequentially observed independent events the last event satisfying a specific criterion (a "specific event"). This identification must be done at the time of observation. No revisiting of preceding observations is permitted. Usually, a specific
event is defined by the decision maker as an event that is of true interest in the view of "stopping" to take a well-defined action. Such problems are encountered in several situations.
Examples
Two different situations exemplify the interest in maximizing the probability to stop on a last specific event.- Suppose a car is advertised for sale to the highest bidder (best "offer"). n potential buyers respond and ask to see the car. Each insists upon an immediate decision from the seller to accept the bid, or not. Define a bid as interesting, and coded 1 if it is better than all preceding bids, and coded 0 otherwise. The bids will form a random sequence of 0s and 1s. Only 1s interest the seller, who may fear that each successive 1 might be the last. It follows from the definition that the very last 1 is the highest bid. Maximizing the probability of selling on the last 1 therefore means maximizing the probability of selling best.
- A physician, using a special treatment, may use the code 1 for a successful treatment, 0 otherwise. The physician treats a sequence of n patients the same way, and wants to minimize any suffering, and to achieve success with every patient in the sequence. Stopping on the last 1 in such a random sequence of 0s and 1s would achieve this objective. Since the physician is no prophet, the objective is to maximize the probability of stopping on the last 1.
Definitions
Consider a sequence of n independent events. Associate with this sequence another sequence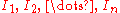 with values 1 or 0. Here 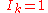stands forthe event that the kth observation is interesting (as defined by the decision maker), and
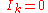for non-interesting.Let
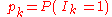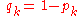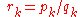be the probability that the kth event is interesting. Further let and . Note that 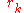represents the oddsOdds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
of the kth event turning out to be interesting,
explaining the name of the odds-algorithm.
Algorithmic procedure of the odds-algorithm
The odds-algorithm sums up the odds in reverse order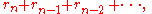until this sum reaches or exceeds the value 1 for the first time. If this happens at index s, it saves s and the corresponding sum
If the sum of the odds does not reach 1, it sets s = 1. At the same time it computes
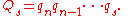
The output is
-
, the stopping threshold -
, the win probability.
Odds-strategy
The odds-strategy is the rule to observe the events one after the other and to stopon the first interesting event from index s onwards (if any), where s is the stopping threshold of output a).
The importance of the odds-strategy, and hence of the odds-algorithm, lies in the following odds-theorem.
Odds-theorem
The odds-theorem states that- The odds-strategy is optimal, that is, it maximizes the probability of stopping on the last 1.
- The win probability of the odds-strategy equals
- If
, the win probability 
is always at least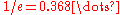 
, and this lower bound is best possible.
Features of the odds-algorithm
The odds-algorithm computes the optimal strategy and the optimal win probability at the same time. Also, the number of operations of the odds-algorithm is (sub)linear in n. Hence no quicker algorithm can possiblyexist for all sequences, so that the odds-algorithm is, at the same time, optimal as an algorithm.
Source
F. T. Bruss (2000) devised the odds algorithm, and coined its name. It is also known as Bruss-algorithm (strategy). Free implementations can be found on the web.Applications
Applications reach from medical questions in clinical trialClinical trial
Clinical trials are a set of procedures in medical research and drug development that are conducted to allow safety and efficacy data to be collected for health interventions...
s over sales problems, secretary problems, portfolio
Portfolio (finance)
Portfolio is a financial term denoting a collection of investments held by an investment company, hedge fund, financial institution or individual.-Definition:The term portfolio refers to any collection of financial assets such as stocks, bonds and cash...
selection, (one-way) search strategies, trajectory problems and the parking problem to problems in on-line maintenance and others.
There exists, in the same spirit, an Odds-Theorem for continuous-time arrival processes with independent increments such as the Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
(Bruss (2000)). In some cases, the odds are not necessarily known in advance (as in Example 2 above) so that the application of the odds-algorithm is not directly possible. In this case each step can use sequential estimates of the odds. This is meaningful, if the number of unknown parameters is not large compared with the number n of observations. The question of optimality is then more complicated, however, and requires additional studies. Generalizations of the odds-algorithm allow for different rewards for failing to stop
and wrong stops as well as replacing independence assumptions by weaker ones (Ferguson (2008)).
See also
- Secretary problemSecretary problemThe secretary problem is one of many names for a famous problem of theoptimal stopping theory.The problem has been studied extensively in the fields ofapplied probability, statistics, and decision theory...
- Clinical trialClinical trialClinical trials are a set of procedures in medical research and drug development that are conducted to allow safety and efficacy data to be collected for health interventions...
- Maintenance, repair and operationsMaintenance, Repair and OperationsMaintenance, repair, and operations or maintenance, repair, and overhaul involves fixing any sort of mechanical or electrical device should it become out of order or broken...
- House selling problem
- Parking problem
External links
- Bruss-Algorithmus http://www.p-roesler.de/odds.html
- Sports Picks eXpert System – Prediction Algorithm http://www.amcomputersystems.com/spxs/odds_algorithm.php