Optimal stopping
Encyclopedia
In mathematics
, the theory of optimal stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise
an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics
, economics
, and mathematical finance
(related to the pricing of American options). A key example of an optimal stopping problem is the secretary problem
. Optimal stopping problems can often be written in the form of a Bellman equation
, and are therefore often solved using dynamic programming
.
Given those objects, the problem is as follows:
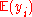converges)
You have a fair coin and are repeatedly tossing it. Each time, before it is tossed, you can choose to stop tossing it and get paid (in dollars, say) the average number of heads observed.
You wish to maximise the amount you get paid by choosing a stopping rule.
If Xi (for i ≥ 1) forms a sequence of independent, identically distributed random variables with distribution
and if
then the sequences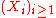
, and 
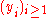are the objects associated with this problem.
House selling (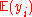
does not necessarily converge)
You have a house and wish to sell it. Each day you are offered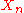
for your house, and pay 
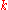to continue advertising it. If you sell your house on day 
, you will earn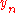 
, where 
.
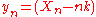You wish to maximise the amount you earn by choosing a stopping rule.
In this example, the sequence (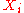
) is the sequence of offers for your house, and the sequence of reward functions is how much you will earn.
Secretary problem (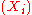
is a finite sequence)
You are observing a sequence of objects which can be ranked from best to worst. You wish to choose a stopping rule which maximises your chance of picking the best object.
Here, if
(n is some large number, perhaps) are the ranks of the objects, and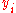 
is the chance you pick the best object if you stop intentionally rejecting objects at step i, then 
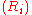and 
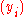are the sequences associated with this problem. This problem was solved in the early 1960s by several people. An elegant solution to the secretary problem and several modifications of this problem is provided by the more recent odds algorithm
of optimal stopping (Bruss algorithm).
Search theory
Economists have studied a number of optimal stopping problems similar to the 'secretary problem', and typically call this type of analysis 'search theory'. Search theory has especially focused on a worker's search for a high-wage job, or a consumer's search for a low-priced good.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the theory of optimal stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, and mathematical finance
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
(related to the pricing of American options). A key example of an optimal stopping problem is the secretary problem
Secretary problem
The secretary problem is one of many names for a famous problem of theoptimal stopping theory.The problem has been studied extensively in the fields ofapplied probability, statistics, and decision theory...
. Optimal stopping problems can often be written in the form of a Bellman equation
Bellman equation
A Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
, and are therefore often solved using dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
.
Definition
Stopping rule problems are associated with two objects:- A sequence of random variables
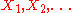, whose joint distribution is something assumed to be known
- A sequence of 'reward' functions
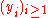which depend on the observed values of the random variables in 1.:
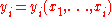
Given those objects, the problem is as follows:
- You are observing the sequence of random variables, and at each step
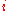, you can choose to either stop observing or continue - If you stop observing at step
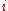, you will receive reward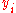 
- You want to choose a stopping ruleStopping ruleIn probability theory, in particular in the study of stochastic processes, a stopping time is a specific type of “random time”....
to maximise your expected reward (or equivalently, minimise your expected loss)
Examples
Coin tossing (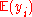 converges)You have a fair coin and are repeatedly tossing it. Each time, before it is tossed, you can choose to stop tossing it and get paid (in dollars, say) the average number of heads observed.
You wish to maximise the amount you get paid by choosing a stopping rule.
If Xi (for i ≥ 1) forms a sequence of independent, identically distributed random variables with distribution
and if
then the sequences
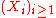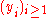, and are the objects associated with this problem.House selling (
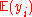does not necessarily converge)You have a house and wish to sell it. Each day you are offered
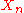for your house, and pay 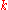to continue advertising it. If you sell your house on day , you will earn 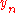, where 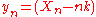.You wish to maximise the amount you earn by choosing a stopping rule.
In this example, the sequence (
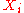) is the sequence of offers for your house, and the sequence of reward functions is how much you will earn.Secretary problem (
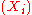is a finite sequence)You are observing a sequence of objects which can be ranked from best to worst. You wish to choose a stopping rule which maximises your chance of picking the best object.
Here, if
(n is some large number, perhaps) are the ranks of the objects, and 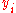is the chance you pick the best object if you stop intentionally rejecting objects at step i, then 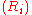and 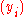are the sequences associated with this problem. This problem was solved in the early 1960s by several people. An elegant solution to the secretary problem and several modifications of this problem is provided by the more recent odds algorithmOdds algorithm
The odds-algorithm is a mathematical method for computing optimalstrategies for a class of problems that belong to the domain of optimal stopping problems. Their solution follows from the odds-strategy, and the importance of the...
of optimal stopping (Bruss algorithm).
Search theory
Economists have studied a number of optimal stopping problems similar to the 'secretary problem', and typically call this type of analysis 'search theory'. Search theory has especially focused on a worker's search for a high-wage job, or a consumer's search for a low-priced good.