Oja's rule
Encyclopedia
Oja's learning rule, or simply Oja's rule, named after a Finnish computer scientist Erkki Oja
, is a model of how neurons in the brain or in artificial neural networks change connection strength, or learn, over time. It is a modification of the standard Hebb's Rule (see Hebbian learning) that, through multiplicative normalization, solves all stability problems and generates an algorithm for principal components analysis
. This is a computational form of an effect which is believed to happen in biological neurons.
. However, Oja's rule can also be generalized in other ways to varying degrees of stability and success.
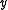of a neuron to its inputs to be
where is the learning rate which can also change with time. Note that the bold symbols are vectors and defines a discrete time iteration. The rule can also be made for continuous iterations as
,
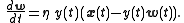
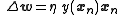or with implicit -dependence,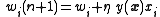
,
where is again the output, this time explicitly dependent on its input vector .
Hebb's rule has synaptic weights approaching infinity with a positive learning rate. We can stop this by normalizing the weights so that each weight's magnitude is restricted between 0, corresponding to no weight, and 1, corresponding to being the only input neuron with any weight. Mathematically, this takes the form
.
Note that in Oja's original paper, , corresponding to quadrature (root sum of squares), which is the familiar Cartesian normalization rule. However, any type of normalization, even linear, will give the same result without loss of generality.
Our next step is to expand this into a Taylor series
for a small learning rate
, giving
.
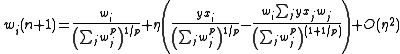For small , our higher-order terms go to zero. We again make the specification of a linear neuron, that is, the output of the neuron is equal to the sum of the product of each input and its synaptic weight, or
.
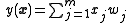We also specify that our weights normalize to , which will be a necessary condition for stability, so
,
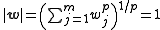which, when substituted into our expansion, gives Oja's rule, or
.
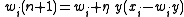, one can create a multi-Oja neural network that can extract as many features as desired, allowing for principal components analysis
.
A principal component is extracted from a dataset through some associated vector , or , and we can restore our original dataset by taking
.
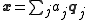In the case of a single neuron trained by Oja's rule, we find the weight vector converges to , or the first principal component, as time or number of iterations approaches infinity. We can also define, given a set of input vectors , that its correlation matrix has an associated eigenvector given by with eigenvalue . The variance
of outputs of our Oja neuron then converges with time iterations to the principal eigenvalue, or
.
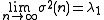These results are derived using Lyapunov function
analysis, and they show that Oja's neuron necessarily converges on strictly the first principal component if certain conditions are met in our original learning rule. Most importantly, our learning rate is allowed to vary with time, but only such that its sum is divergent but its power sum is convergent, that is
.
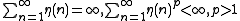Our output activation function
is also allowed to be nonlinear and nonstatic, but it must be continuously differentiable in both and and have derivatives bounded in time.
in 1952. PCA has also had a long history of use before Oja's rule formalized its use in network computation in 1989. The model can thus be applied to any problem of self-organizing map
ping, in particular those in which feature extraction is of primary interest. Therefore, Oja's rule has an important place in image and speech processing. It is also useful as it expands easily to higher dimensions of processing, thus being able to integrate multiple outputs quickly. A canonical example is its use in binocular vision
.
and long-term depression
in biological neural networks, along with a normalization effect in both input weights and neuron outputs. However, while as of yet there is no direct experimental evidence of Oja's rule active in a biological neural network, a biophysical
derivation of a generalization of the rule is possible. Such a derivation requires retrograde signalling from the postsynaptic neuron, which is biologically plausible (see neural backpropagation
), and takes the form of
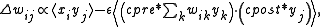
where as before is the synaptic weight between the th input and th output neurons, is the input, is the postsynaptic output, and we define to be a constant analogous the learning rate, and and are presynaptic and postsynaptic functions that model the weakening of signals over time. Note that the angle brackets denote the average and the operator is a convolution
. By taking the pre- and post-synaptic functions into frequency space and combining integration terms with the convolution, we find that this gives an arbitrary-dimensional generalization of Oja's rule known as Oja's Subspace, namely
Erkki Oja
Erkki Oja is a Finnish computer scientist. He is a professor at the Department of Information and Computer Science at Aalto University School of Science and Technology, the director of the Adaptive Informatics Research Centre and chairman of the Academy of Finland's Research Council for Natural...
, is a model of how neurons in the brain or in artificial neural networks change connection strength, or learn, over time. It is a modification of the standard Hebb's Rule (see Hebbian learning) that, through multiplicative normalization, solves all stability problems and generates an algorithm for principal components analysis
Principal components analysis
Principal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
. This is a computational form of an effect which is believed to happen in biological neurons.
Theory
Oja's rule requires a number of simplifications to derive, but in its final form it is demonstrably stable, unlike Hebb's rule. It is a single-neuron special case of the Generalized Hebbian AlgorithmGeneralized Hebbian Algorithm
The Generalized Hebbian Algorithm , also known in the literature as Sanger's rule, is a linear feedforward neural network model for unsupervised learning with applications primarily in principal components analysis...
. However, Oja's rule can also be generalized in other ways to varying degrees of stability and success.
Formula
Oja's rule defines the change in presynaptic weights given the output response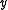 of a neuron to its inputs to bewhere is the learning rate which can also change with time. Note that the bold symbols are vectors and defines a discrete time iteration. The rule can also be made for continuous iterations as
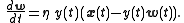
Derivation
The simplest learning rule known is Hebb's rule, which states in conceptual terms that neurons that fire together, wire together. In component form as a difference equation, it is written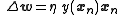,or with implicit -dependence,
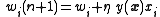,where is again the output, this time explicitly dependent on its input vector .
Hebb's rule has synaptic weights approaching infinity with a positive learning rate. We can stop this by normalizing the weights so that each weight's magnitude is restricted between 0, corresponding to no weight, and 1, corresponding to being the only input neuron with any weight. Mathematically, this takes the form
.Note that in Oja's original paper, , corresponding to quadrature (root sum of squares), which is the familiar Cartesian normalization rule. However, any type of normalization, even linear, will give the same result without loss of generality.
Our next step is to expand this into a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for a small learning rate
, giving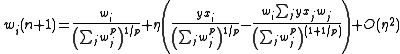.For small , our higher-order terms go to zero. We again make the specification of a linear neuron, that is, the output of the neuron is equal to the sum of the product of each input and its synaptic weight, or
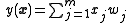.We also specify that our weights normalize to , which will be a necessary condition for stability, so
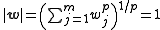,which, when substituted into our expansion, gives Oja's rule, or
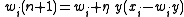.Stability and PCA
In analyzing the convergence of a single neuron evolving by Oja's rule, one extracts the first principal component, or feature, of a data set. Furthermore, with extensions using the Generalized Hebbian AlgorithmGeneralized Hebbian Algorithm
The Generalized Hebbian Algorithm , also known in the literature as Sanger's rule, is a linear feedforward neural network model for unsupervised learning with applications primarily in principal components analysis...
, one can create a multi-Oja neural network that can extract as many features as desired, allowing for principal components analysis
Principal components analysis
Principal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
.
A principal component is extracted from a dataset through some associated vector , or , and we can restore our original dataset by taking
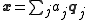.In the case of a single neuron trained by Oja's rule, we find the weight vector converges to , or the first principal component, as time or number of iterations approaches infinity. We can also define, given a set of input vectors , that its correlation matrix has an associated eigenvector given by with eigenvalue . The variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of outputs of our Oja neuron then converges with time iterations to the principal eigenvalue, or
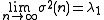.These results are derived using Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
analysis, and they show that Oja's neuron necessarily converges on strictly the first principal component if certain conditions are met in our original learning rule. Most importantly, our learning rate is allowed to vary with time, but only such that its sum is divergent but its power sum is convergent, that is
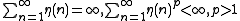.Our output activation function
Activation function
In computational networks, the activation function of a node defines the output of that node given an input or set of inputs. A standard computer chip circuit can be seen as a digital network of activation functions that can be "ON" or "OFF" , depending on input. This is similar to the behavior of...
is also allowed to be nonlinear and nonstatic, but it must be continuously differentiable in both and and have derivatives bounded in time.
Applications
Oja's rule was originally described in Oja's 1982 paper, but the principle of self-organization to which it is applied is first attributed to Alan TuringAlan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
in 1952. PCA has also had a long history of use before Oja's rule formalized its use in network computation in 1989. The model can thus be applied to any problem of self-organizing map
Self-organizing map
A self-organizing map or self-organizing feature map is a type of artificial neural network that is trained using unsupervised learning to produce a low-dimensional , discretized representation of the input space of the training samples, called a map...
ping, in particular those in which feature extraction is of primary interest. Therefore, Oja's rule has an important place in image and speech processing. It is also useful as it expands easily to higher dimensions of processing, thus being able to integrate multiple outputs quickly. A canonical example is its use in binocular vision
Binocular vision
Binocular vision is vision in which both eyes are used together. The word binocular comes from two Latin roots, bini for double, and oculus for eye. Having two eyes confers at least four advantages over having one. First, it gives a creature a spare eye in case one is damaged. Second, it gives a...
.
Biology and Oja's subspace rule
There is clear evidence for both long-term potentiationLong-term potentiation
In neuroscience, long-term potentiation is a long-lasting enhancement in signal transmission between two neurons that results from stimulating them synchronously. It is one of several phenomena underlying synaptic plasticity, the ability of chemical synapses to change their strength...
and long-term depression
Long-term depression
Long-term depression , in neurophysiology, is an activity-dependent reduction in the efficacy of neuronal synapses lasting hours or longer. LTD occurs in many areas of the CNS with varying mechanisms depending upon brain region and developmental progress...
in biological neural networks, along with a normalization effect in both input weights and neuron outputs. However, while as of yet there is no direct experimental evidence of Oja's rule active in a biological neural network, a biophysical
Biophysics
Biophysics is an interdisciplinary science that uses the methods of physical science to study biological systems. Studies included under the branches of biophysics span all levels of biological organization, from the molecular scale to whole organisms and ecosystems...
derivation of a generalization of the rule is possible. Such a derivation requires retrograde signalling from the postsynaptic neuron, which is biologically plausible (see neural backpropagation
Neural backpropagation
Neural backpropagation is the phenomenon in which the action potential of a neuron creates a voltage spike both at the end of the axon and back through to the dendritic arbor or dendrites, from which much of the original input current originated...
), and takes the form of
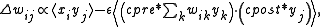
where as before is the synaptic weight between the th input and th output neurons, is the input, is the postsynaptic output, and we define to be a constant analogous the learning rate, and and are presynaptic and postsynaptic functions that model the weakening of signals over time. Note that the angle brackets denote the average and the operator is a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. By taking the pre- and post-synaptic functions into frequency space and combining integration terms with the convolution, we find that this gives an arbitrary-dimensional generalization of Oja's rule known as Oja's Subspace, namely
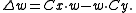
See also
- BCM theoryBCM theoryBCM theory, BCM synaptic modification, or the BCM rule, named for Elie Bienenstock, Leon Cooper, and Paul Munro, is a physical theory of learning in the visual cortex developed in 1981...
- Synaptic plasticitySynaptic plasticityIn neuroscience, synaptic plasticity is the ability of the connection, or synapse, between two neurons to change in strength in response to either use or disuse of transmission over synaptic pathways. Plastic change also results from the alteration of the number of receptors located on a synapse...
- Self-organizing mapSelf-organizing mapA self-organizing map or self-organizing feature map is a type of artificial neural network that is trained using unsupervised learning to produce a low-dimensional , discretized representation of the input space of the training samples, called a map...
- Principal components analysisPrincipal components analysisPrincipal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
- Independent components analysis