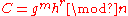Okamoto-Uchiyama cryptosystem
Encyclopedia
The Okamoto–Uchiyama cryptosystem was discovered in 1998 by T. Okamoto and S. Uchiyama. The system works in the group 
, where n is of the form p2q and p and q are large primes
.
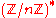. A fundamental difference of this cryptosystem is that here n is a of the form p2q, where p and q are large primes
. This scheme is homomorphic
and hence malleable
.
The public key is then (n, g, h) and the private key is the factors (p, q).
, then decryption becomes
.
The group
has a unique subgroup of order p, call it H.
By the uniqueness of H, we must have
.
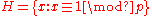For any element x in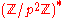
, we have xp−1 mod p2 is in H, since p divides xp−1 − 1.
The map L should be thought of as a logarithm from the cyclic group H to the additive group
, and it is easy to check that L(ab) = L(a) + L(b), and that the L is an isomorphism between these two groups. As is the case with the usual logarithm, L(x)/L(g) is, in a sense, the logarithm of x with base g.
We have
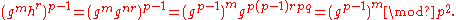
So to recover m we just need to take the logarithm with base gp−1, which is accomplished by
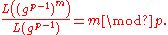
rests on the p-subgroup assumption, which assumes that it is difficult to determine whether an element x in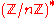
is in the subgroup of order p. This is very similar to the quadratic residuosity problem
and the higher residuosity problem
.
, where n is of the form p2q and p and q are large primesPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
.
Scheme definition
Like many public key cryptosystems, this scheme works in the group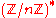. A fundamental difference of this cryptosystem is that here n is a of the form p2q, where p and q are large primesPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. This scheme is homomorphic
Homomorphic encryption
Homomorphic encryption is a form of encryption where a specific algebraic operation performed on the plaintext is equivalent to another algebraic operation performed on the ciphertext. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem....
and hence malleable
Malleability (cryptography)
Malleability is a property of some cryptographic algorithms. An encryption algorithm is malleable if it is possible for an adversary to transform a ciphertext into another ciphertext which decrypts to a related plaintext...
.
Key generation
A public/private key pair is generated as follows:- Generate large primes p and q and set
. - Choose
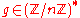such that 
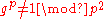. - Let h = gn mod n.
The public key is then (n, g, h) and the private key is the factors (p, q).
Message encryption
To encrypt a message m, where m is taken to be an element in- Select
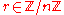at random. Set
Message decryption
If we define, then decryption becomesHow the system works
The group.The group
has a unique subgroup of order p, call it H.By the uniqueness of H, we must have
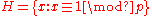.For any element x in
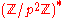, we have xp−1 mod p2 is in H, since p divides xp−1 − 1.The map L should be thought of as a logarithm from the cyclic group H to the additive group
, and it is easy to check that L(ab) = L(a) + L(b), and that the L is an isomorphism between these two groups. As is the case with the usual logarithm, L(x)/L(g) is, in a sense, the logarithm of x with base g.We have
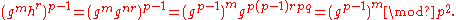
So to recover m we just need to take the logarithm with base gp−1, which is accomplished by
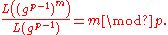
Security
The security of the entire message can be shown to be equivalent to factoring n. The semantic securitySemantic security
Semantic security is a widely used definition for security in an asymmetric key encryption algorithm. For a cryptosystem to be semantically secure, it must be infeasible for a computationally bounded adversary to derive significant information about a message when given only its ciphertext and...
rests on the p-subgroup assumption, which assumes that it is difficult to determine whether an element x in
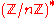is in the subgroup of order p. This is very similar to the quadratic residuosity problemQuadratic residuosity problem
The quadratic residuosity problem in computational number theory is the question of distinguishing by calculating the quadratic residues modulo N, where N is a composite number...
and the higher residuosity problem
Higher residuosity problem
In cryptography most public key cryptosystems are founded on problems that are believed to be intractable. The higher residuosity problem is one such problem...
.