
Omega equation
Encyclopedia
The omega equation is of great importance in meteorology
and atmospheric physics
. It is a partial differential equation
for the vertical velocity,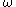 , which is defined as a Lagrangian
, which is defined as a Lagrangian
rate of change of pressure with time, that is,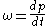 .
.
The equation reads:
where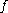 is the Coriolis parameter,
is the Coriolis parameter,  is the static stability,
is the static stability, 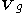 is the geostrophic velocity vector,
is the geostrophic velocity vector, 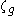 is the geostrophic relative vorticity,
is the geostrophic relative vorticity, 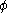 is the geopotential
is the geopotential
,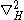 is the horizontal Laplacian operator and
is the horizontal Laplacian operator and  is the horizontal del
is the horizontal del
operator .
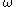 equation is based on the vorticity equation
equation is based on the vorticity equation
and the thermodynamic equation. The vorticity equation
for a frictionless atmosphere may be written as:
Here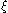 is the relative vorticity,
is the relative vorticity, 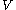 the horizontal wind velocity vector, whose components in the
the horizontal wind velocity vector, whose components in the  and
and 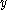 directions are
directions are  and
and  respectively,
respectively, 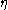 the absolute vorticity,
the absolute vorticity, 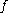 the Coriolis parameter
the Coriolis parameter
,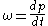 the individual rate of change of pressure
the individual rate of change of pressure 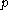 .
.  is the unit vertical vector,
is the unit vertical vector, 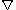 is the isobaric Del (grad) operator,
is the isobaric Del (grad) operator, 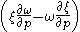 is the vertical
is the vertical
advection of vorticity and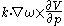 represents the transformation of horizontal vorticity into vertical vorticity .
represents the transformation of horizontal vorticity into vertical vorticity .
The thermodynamic equation may be written as:
where , in which
, in which 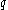 is the supply of heat per unit-time and mass,
is the supply of heat per unit-time and mass, 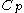 the specific heat of dry air,
the specific heat of dry air, 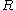 the gas constant for dry air,
the gas constant for dry air, 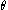 is the potential temperature and
is the potential temperature and  is geopotential
is geopotential 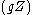 .
.
The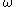 equation is then obtained from equation and by substituting values:
equation is then obtained from equation and by substituting values:
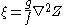
and
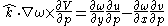
into , which gives:
Differentiating with respect to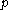 gives:
gives:
Taking the Laplacian ( ) of gives:
) of gives:
Adding and , simplifying and substituting , gives:
, gives:
Equation is now a linear differential equation in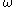 , such that it can be split into two part, namely
, such that it can be split into two part, namely 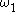 and
and  , such that:
, such that:
and
where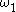 is the vertical velocity due to the mean baroclinicity in the atmosphere and
is the vertical velocity due to the mean baroclinicity in the atmosphere and 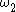 is the vertical velocity due to the non-adiabatic heating, which includes the latent heat of condensation, sensible heat radiation, etc. (Singh & Rathor, 1974).
is the vertical velocity due to the non-adiabatic heating, which includes the latent heat of condensation, sensible heat radiation, etc. (Singh & Rathor, 1974).
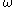 .)
.)
The above equation is used by meteorologists and operational weather forecasters to assess development from synoptic charts. In rather simple terms, positive vorticity advection (or PVA for short) and no thermal advection results in a negative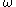 , that is, ascending motion. Similarly, warm advection (or WA for short) also results in a negative
, that is, ascending motion. Similarly, warm advection (or WA for short) also results in a negative 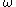 corresponding to ascending motion. Negative vorticity advection (NVA) or cold advection (CA) both result in a positive
corresponding to ascending motion. Negative vorticity advection (NVA) or cold advection (CA) both result in a positive 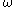 corresponding to descending motion.
corresponding to descending motion.
Meteorology
Meteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
and atmospheric physics
Atmospheric physics
Atmospheric physics is the application of physics to the study of the atmosphere. Atmospheric physicists attempt to model Earth's atmosphere and the atmospheres of the other planets using fluid flow equations, chemical models, radiation balancing, and energy transfer processes in the atmosphere...
. It is a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
for the vertical velocity,
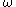 , which is defined as a Lagrangian
, which is defined as a LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
rate of change of pressure with time, that is,
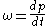 .
.The equation reads:
where
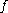 is the Coriolis parameter,
is the Coriolis parameter,  is the static stability,
is the static stability, 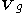 is the geostrophic velocity vector,
is the geostrophic velocity vector, 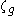 is the geostrophic relative vorticity,
is the geostrophic relative vorticity, 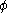 is the geopotential
is the geopotentialGeopotential
Geopotential is the potential of the Earth's gravity field. For convenience it is often defined as minus the potential energy per unit mass, so that the gravity vector is obtained as the gradient of this potential, without the minus....
,
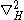 is the horizontal Laplacian operator and
is the horizontal Laplacian operator and  is the horizontal del
is the horizontal delDel
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
operator .
Derivation
The derivation of the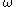 equation is based on the vorticity equation
equation is based on the vorticity equationVorticity equation
The vorticity equation is an important prognostic equation in the atmospheric sciences. Vorticity is a vector, therefore, there are three components...
and the thermodynamic equation. The vorticity equation
Vorticity equation
The vorticity equation is an important prognostic equation in the atmospheric sciences. Vorticity is a vector, therefore, there are three components...
for a frictionless atmosphere may be written as:
Here
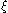 is the relative vorticity,
is the relative vorticity, 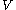 the horizontal wind velocity vector, whose components in the
the horizontal wind velocity vector, whose components in the  and
and 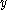 directions are
directions are  and
and  respectively,
respectively, 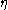 the absolute vorticity,
the absolute vorticity, 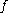 the Coriolis parameter
the Coriolis parameterCoriolis frequency
The Coriolis frequency ƒ, also called the Coriolis parameter or Coriolis coefficient, is equal to twice the rotation rate Ω of the Earth multiplied by the sine of the latitude φ.f = 2 \Omega \sin \varphi.\,...
,
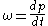 the individual rate of change of pressure
the individual rate of change of pressure 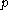 .
.  is the unit vertical vector,
is the unit vertical vector, 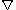 is the isobaric Del (grad) operator,
is the isobaric Del (grad) operator, 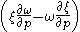 is the vertical
is the verticaladvection of vorticity and
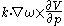 represents the transformation of horizontal vorticity into vertical vorticity .
represents the transformation of horizontal vorticity into vertical vorticity .The thermodynamic equation may be written as:
where
 , in which
, in which 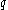 is the supply of heat per unit-time and mass,
is the supply of heat per unit-time and mass, 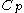 the specific heat of dry air,
the specific heat of dry air, 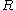 the gas constant for dry air,
the gas constant for dry air, 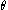 is the potential temperature and
is the potential temperature and  is geopotential
is geopotential 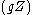 .
.The
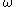 equation is then obtained from equation and by substituting values:
equation is then obtained from equation and by substituting values: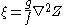
and
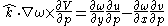
into , which gives:
Differentiating with respect to
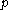 gives:
gives:Taking the Laplacian (
 ) of gives:
) of gives:Adding and , simplifying and substituting
 , gives:
, gives:Equation is now a linear differential equation in
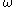 , such that it can be split into two part, namely
, such that it can be split into two part, namely 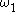 and
and  , such that:
, such that:and
where
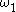 is the vertical velocity due to the mean baroclinicity in the atmosphere and
is the vertical velocity due to the mean baroclinicity in the atmosphere and 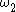 is the vertical velocity due to the non-adiabatic heating, which includes the latent heat of condensation, sensible heat radiation, etc. (Singh & Rathor, 1974).
is the vertical velocity due to the non-adiabatic heating, which includes the latent heat of condensation, sensible heat radiation, etc. (Singh & Rathor, 1974).Interpretation
Physically, the omega equation combines the effects of vertical differential of geostrophic absolute vorticity advection (first term on the right-hand side) and three-dimensional Laplacian of thickness thermal advection (second term on the right-hand side) and determines the resulting vertical motion (as expressed by the dependent variable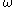 .)
.)The above equation is used by meteorologists and operational weather forecasters to assess development from synoptic charts. In rather simple terms, positive vorticity advection (or PVA for short) and no thermal advection results in a negative
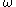 , that is, ascending motion. Similarly, warm advection (or WA for short) also results in a negative
, that is, ascending motion. Similarly, warm advection (or WA for short) also results in a negative 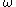 corresponding to ascending motion. Negative vorticity advection (NVA) or cold advection (CA) both result in a positive
corresponding to ascending motion. Negative vorticity advection (NVA) or cold advection (CA) both result in a positive 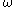 corresponding to descending motion.
corresponding to descending motion.
