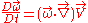Vorticity equation
Encyclopedia
The vorticity equation is an important prognostic equation in the atmospheric sciences
. Vorticity is a vector, therefore, there are three components. The equation of vorticity (three components in the canonical form) describes the material derivative (that is, the local change due to local change with time and advection
) of vorticity, and thus can be stated in either relative or absolute form.
The more compact version is that for absolute vorticity, component , using the pressure system:
, using the pressure system:
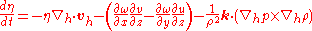
Here, is density
is density
, u, v, and are the components of wind velocity
are the components of wind velocity
, and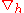 is the 2-dimensional (i.e. horizontal-component-only) del
is the 2-dimensional (i.e. horizontal-component-only) del
.
The terms on the RHS denote the positive or negative generation of absolute vorticity by divergence
of air, twisting of the axis of rotation, and baroclinity
, respectively.
 of a fluid element as it moves around. The vorticity equation can be derived from the conservation of momentum equation. In its general vector form it may be expressed as follows,
of a fluid element as it moves around. The vorticity equation can be derived from the conservation of momentum equation. In its general vector form it may be expressed as follows,
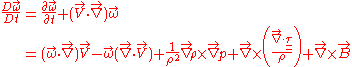
where, is the velocity vector,
is the velocity vector, 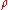 is the density,
is the density, 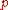 is the pressure,
is the pressure, 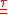 is the viscous stress tensor and
is the viscous stress tensor and  is the body force term.
is the body force term.
Equivalently in tensor notation,

where, we have used the Einstein summation convention
, and is the Levi-Civita symbol
is the Levi-Civita symbol
.
Thus for an inviscid, barotropic fluid with conservative body forces, the vorticity equation simplifies to,
Alternately, in case of incompressible, inviscid fluid with conservative body forces,
Atmospheric sciences
Atmospheric sciences is an umbrella term for the study of the atmosphere, its processes, the effects other systems have on the atmosphere, and the effects of the atmosphere on these other systems. Meteorology includes atmospheric chemistry and atmospheric physics with a major focus on weather...
. Vorticity is a vector, therefore, there are three components. The equation of vorticity (three components in the canonical form) describes the material derivative (that is, the local change due to local change with time and advection
Advection
Advection, in chemistry, engineering and earth sciences, is a transport mechanism of a substance, or a conserved property, by a fluid, due to the fluid's bulk motion in a particular direction. An example of advection is the transport of pollutants or silt in a river. The motion of the water carries...
) of vorticity, and thus can be stated in either relative or absolute form.
The more compact version is that for absolute vorticity, component
 , using the pressure system:
, using the pressure system: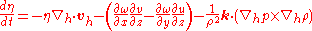
Here,
 is density
is densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, u, v, and
 are the components of wind velocity
are the components of wind velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, and
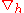 is the 2-dimensional (i.e. horizontal-component-only) del
is the 2-dimensional (i.e. horizontal-component-only) delDel
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
.
The terms on the RHS denote the positive or negative generation of absolute vorticity by divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of air, twisting of the axis of rotation, and baroclinity
Baroclinity
In fluid dynamics, the baroclinity of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid...
, respectively.
Fluid dynamics
The vorticity equation describes the evolution of the vorticity of a fluid element as it moves around. The vorticity equation can be derived from the conservation of momentum equation. In its general vector form it may be expressed as follows,
of a fluid element as it moves around. The vorticity equation can be derived from the conservation of momentum equation. In its general vector form it may be expressed as follows,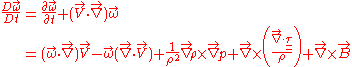
where,
 is the velocity vector,
is the velocity vector, 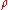 is the density,
is the density, 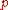 is the pressure,
is the pressure, 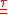 is the viscous stress tensor and
is the viscous stress tensor and  is the body force term.
is the body force term.Equivalently in tensor notation,

where, we have used the Einstein summation convention
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
, and
 is the Levi-Civita symbol
is the Levi-Civita symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
.
Physical Interpretation
- The term
 is the material derivative of the vorticity vector
is the material derivative of the vorticity vector 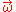 . It describes the rate of change of vorticity of a fluid particle (or in other words the angular acceleration of the fluid particle). This can change due to the unsteadiness in the flow captured by
. It describes the rate of change of vorticity of a fluid particle (or in other words the angular acceleration of the fluid particle). This can change due to the unsteadiness in the flow captured by  (the unsteady term) or due to the motion of the fluid particle as it moves from one point to another,
(the unsteady term) or due to the motion of the fluid particle as it moves from one point to another,  (the convection term).
(the convection term).
- The first term on the RHS of the vorticity equation,
 , describes the stretching or tilting of vorticity due to the velocity gradients. Note that
, describes the stretching or tilting of vorticity due to the velocity gradients. Note that  is a tensor with nine terms.
is a tensor with nine terms.
- The next term,
 , describes stretching of vorticityVortex stretchingIn fluid dynamics, vortex stretching is the lengthening of vortices in three-dimensional fluid flow, associated with a corresponding increase of the component of vorticity in the stretching direction—due to the conservation of angular momentum....
, describes stretching of vorticityVortex stretchingIn fluid dynamics, vortex stretching is the lengthening of vortices in three-dimensional fluid flow, associated with a corresponding increase of the component of vorticity in the stretching direction—due to the conservation of angular momentum....
due to flow compressibility. Sometimes the negative sign is included in the term.
- The third term,
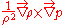 is the baroclinic term. It accounts for the changes in the vorticity due to the intersection of density and pressure surfaces.
is the baroclinic term. It accounts for the changes in the vorticity due to the intersection of density and pressure surfaces.
-
 , accounts for the diffusion of vorticity due to the viscous effects.
, accounts for the diffusion of vorticity due to the viscous effects.
-
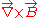 provides for changes due to body forces.
provides for changes due to body forces.
Simplifications
- In case of conservative body forcesConservative forceA conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
, .
. - For a barotropic fluidBarotropicIn meteorology, a barotropic atmosphere is one in which the pressure depends only on the density and vice versa, so that isobaric surfaces are also isopycnic surfaces . The isobaric surfaces will also be isothermal surfaces, hence the geostrophic wind is independent of height...
, . This is also true for a constant density fluid where
. This is also true for a constant density fluid where 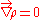 .
. - For inviscid fluids,
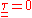 .
.
Thus for an inviscid, barotropic fluid with conservative body forces, the vorticity equation simplifies to,
Alternately, in case of incompressible, inviscid fluid with conservative body forces,