Omega language
Encyclopedia
An ω-language is a set of infinite-length sequences of symbols
.
theory, Σ* is the set of all finite words over Σ. Every finite word has a length, which is, obviously, a natural number. Given a word w of length n, w can be viewed as a function from the set {0,1,...,n-1} → Σ. The infinite words, or ω-words, can likewise be viewed as functions from
to Σ, with the value at i giving the symbol at position i. The set of all infinite words over Σ is denoted Σω. The set of all finite and infinite words over Σ is sometimes written Σ∞.
Thus, an ω-language L over Σ is a subset
of Σω.
by definition of the metric
d:Σω × Σω → R as:
where |x| is interpreted as "the length of x" (number of symbols in x), and inf is the infimum
over sets of real number
s. If w=v, they have no longest finite prefix, and d(w,v)=0; it can be shown that d satisfies all the other necessary properties of a metric
.
, which enjoy the useful property of being recognizable by Büchi automata
; thus the decision problem
of ω-regular language membership is decidable and fairly straightforward to compute.
Symbol (formal)
For other uses see Symbol In logic, symbols build literal utility to illustrate ideas. A symbol is an abstraction, tokens of which may be marks or a configuration of marks which form a particular pattern...
.
Formal definition
Let Σ be a set of symbols (not necessarily finite). Following the standard definition from formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
theory, Σ* is the set of all finite words over Σ. Every finite word has a length, which is, obviously, a natural number. Given a word w of length n, w can be viewed as a function from the set {0,1,...,n-1} → Σ. The infinite words, or ω-words, can likewise be viewed as functions from
to Σ, with the value at i giving the symbol at position i. The set of all infinite words over Σ is denoted Σω. The set of all finite and infinite words over Σ is sometimes written Σ∞.Thus, an ω-language L over Σ is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Σω.
Operations
Some common operations defined on ω-languages are:- Intersection and union. Given ω-languages L and M, both L ∪ M and L ∩ M are ω-languages.
- Left catenation. Let L be an ω-language, and K be a language of finite words only. Then K can be catenated on the left only to L to yield the new ω-language KL.
- Omega (infinite iteration). As the notation hints, the operation (
)ω is the infinite version of the Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
operator on finite-length languages. Given a formal language L, Lω is the ω-language of all infinite sequence of words from L; in the functional view, of all functions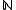
→L. - Prefixes. Let w be an ω-word. Then the formal language Pref(w) contains every finite prefix of w.
- Limit. Given a finite-length language L, an ω-word w is in the limit of L if and only if Pref(w) ∩ L is an infinite set. In other words, for an arbitrarily large natural number n, it is always possible to choose some word in L, whose length is greater than n, and which is a prefix of w. The limit operation on L can be written Lδ or
.
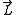Distance between ω-words
The set Σω can be made into a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
by definition of the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
d:Σω × Σω → R as:
- if w and v share any finite prefix, then d(w,v)= inf {2-|x| : x in Σ*, and x in both Pref(w) and Pref(v) }.
- otherwise d(w, v)=1
where |x| is interpreted as "the length of x" (number of symbols in x), and inf is the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
over sets of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. If w=v, they have no longest finite prefix, and d(w,v)=0; it can be shown that d satisfies all the other necessary properties of a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
.
Important subclasses
The most widely-used subclass of the ω-languages is the set of ω-regular languagesOmega-regular language
The ω-regular languages are a class of ω-languages which generalize the definition of regular languages to infinite words. Büchi showed in 1962 that ω-regular languages are precisely the ones definable in a particular monadic second-order logic called S1S.- Formal definition :An...
, which enjoy the useful property of being recognizable by Büchi automata
Büchi automaton
In computer science and automata theory, a Büchi automaton is a type of ω-automaton, which extends a finite automaton to infinite inputs. It accepts an infinite input sequence iff there exists a run of the automaton that visits one of the final states infinitely often. Büchi automata recognize the...
; thus the decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
of ω-regular language membership is decidable and fairly straightforward to compute.