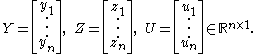Omitted-variable bias
Encyclopedia
In statistics
, omitted-variable bias (OVB) occurs when a model is created which incorrectly leaves out one or more important causal factors. The 'bias' is created when the model compensates for the missing factor by over- or under-estimating one of the other factors.
More specifically, OVB is the bias that appears in the estimates of parameter
s in a regression analysis
, when the assumed specification
is incorrect, in that it omits an independent variable (possibly non-delineated) that should be in the model.
:
As an example, consider a linear model
of the form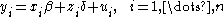
where
We let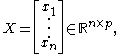
and
Then through the usual least squares
calculation, the estimated parameter vector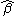
based only on the observed x-values but omitting the observed z values, is given by:
(where the "prime" notation means the transpose of a matrix).
Substituting for Y based on the assumed linear model,
On taking expectations, the contribution of the final term is zero; this follows from the assumption that U has zero expectation. On simplifying the remaining terms: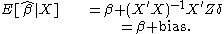
The second term above is the omitted-variable bias in this case. Note that the bias is equal to the weighted portion of zi which is "explained" by xi.
states that regression models which fulfill the classical linear regression model assumptions provide the best, linear and unbiased estimators. With respect to ordinary least squares
, the relevant assumption of the classical linear regression model is that the error term is uncorrelated with the regressors.
The presence of omitted variable bias violates this particular assumption. The violation causes OLS estimator to be biased and inconsistent
. The direction of the biased depends on the estimators as well as the covariance
between the regressors and the omitted variables. Given a positive estimator, a positive covariance will lead OLS estimator to overestimate the true value of an estimator. This effect can be seen by taking the expectation of the parameter, as shown in the previous section.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, omitted-variable bias (OVB) occurs when a model is created which incorrectly leaves out one or more important causal factors. The 'bias' is created when the model compensates for the missing factor by over- or under-estimating one of the other factors.
More specifically, OVB is the bias that appears in the estimates of parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s in a regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
, when the assumed specification
Specification (regression)
In regression analysis and related fields such as econometrics, specification is the process of converting a theory into a regression model. This process consists of selecting an appropriate functional form for the model and choosing which variables to include. Model specification is one of the...
is incorrect, in that it omits an independent variable (possibly non-delineated) that should be in the model.
Omitted-variable bias in linear regression
Two conditions must hold true for omitted-variable bias to exist in linear regressionLinear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
:
- the omitted variable must be a determinant of the dependent variable (i.e., its true regression coefficient is not zero); and
- the omitted variable must be correlated with one or more of the included independent variableIndependent variableThe terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s.
As an example, consider a linear model
Linear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
of the form
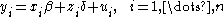
where
- xi is a 1 × p row vector, and is part of the observed data;
- β is a p × 1 column vector of unobservable parameters to be estimated;
- zi is a scalar and is part of the observed data;
- δ is a scalar and is an unobservable parameter to be estimated;
- the error termsErrors and residuals in statisticsIn statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
ui are unobservable random variables having expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
0 (conditionally on xi and zi); - the dependent variables yi are part of the observed data.
We let
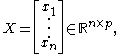
and
Then through the usual least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
calculation, the estimated parameter vector
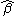based only on the observed x-values but omitting the observed z values, is given by:(where the "prime" notation means the transpose of a matrix).
Substituting for Y based on the assumed linear model,
On taking expectations, the contribution of the final term is zero; this follows from the assumption that U has zero expectation. On simplifying the remaining terms:
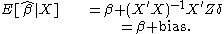
The second term above is the omitted-variable bias in this case. Note that the bias is equal to the weighted portion of zi which is "explained" by xi.
Effects on Ordinary Least Square
Gauss–Markov theoremGauss–Markov theorem
In statistics, the Gauss–Markov theorem, named after Carl Friedrich Gauss and Andrey Markov, states that in a linear regression model in which the errors have expectation zero and are uncorrelated and have equal variances, the best linear unbiased estimator of the coefficients is given by the...
states that regression models which fulfill the classical linear regression model assumptions provide the best, linear and unbiased estimators. With respect to ordinary least squares
Ordinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
, the relevant assumption of the classical linear regression model is that the error term is uncorrelated with the regressors.
The presence of omitted variable bias violates this particular assumption. The violation causes OLS estimator to be biased and inconsistent
Consistency (statistics)
In statistics, consistency of procedures such as confidence intervals or hypothesis tests involves their behaviour as the number of items in the data-set to which they are applied increases indefinitely...
. The direction of the biased depends on the estimators as well as the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
between the regressors and the omitted variables. Given a positive estimator, a positive covariance will lead OLS estimator to overestimate the true value of an estimator. This effect can be seen by taking the expectation of the parameter, as shown in the previous section.