
On shell and off shell
Encyclopedia
In physics
, particularly in quantum field theory
, configurations of a physical system that satisfy classical equations of motion are called on shell, and those that do not are called off shell.
For instance, in classical mechanics
in the action
formulation, extremal solutions to the variational principle
are on shell and the Euler-Lagrange equation
s are on shell equations (i.e., they do not hold off shell). Noether's theorem
is also another on shell theorem.
-momentum
space describing the solutions to the equation

describing combinations of energy E and momentum p allowed by classical special relativity
for a particle of mass m; where is the speed of light
is the speed of light
. The equation for the mass shell is also often written in terms of the four-momentum
, in Einstein notation
and units where c = 1, as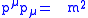 or simply as
or simply as  .
.
Virtual particles corresponding to internal propagator
s in a Feynman diagram
are in general allowed to be off shell, but the amplitude for the process will diminish depending on how far off shell they are; the propagator typically has singularities
on the mass shell.
When speaking of the propagator, negative values for E that satisfy the equation are thought of as being on shell, though the classical theory does not allow negative values for the energy of a particle. This is because the propagator incorporates into one expression the cases in which the particle carries energy in one direction, and in which its antiparticle
carries energy in the other direction; negative and positive on-shell E then simply represent opposing flows of positive energy.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, particularly in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, configurations of a physical system that satisfy classical equations of motion are called on shell, and those that do not are called off shell.
For instance, in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
in the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
formulation, extremal solutions to the variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
are on shell and the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
s are on shell equations (i.e., they do not hold off shell). Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
is also another on shell theorem.
Mass shell
The term comes from the phrase mass shell, which is a synonym for mass hyperboloid, meaning the hyperboloid in energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
-momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
space describing the solutions to the equation

describing combinations of energy E and momentum p allowed by classical special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
for a particle of mass m; where
 is the speed of light
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. The equation for the mass shell is also often written in terms of the four-momentum
Four-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
, in Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
and units where c = 1, as
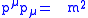 or simply as
or simply as  .
.Virtual particles corresponding to internal propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
s in a Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
are in general allowed to be off shell, but the amplitude for the process will diminish depending on how far off shell they are; the propagator typically has singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
on the mass shell.
When speaking of the propagator, negative values for E that satisfy the equation are thought of as being on shell, though the classical theory does not allow negative values for the energy of a particle. This is because the propagator incorporates into one expression the cases in which the particle carries energy in one direction, and in which its antiparticle
Antiparticle
Corresponding to most kinds of particles, there is an associated antiparticle with the same mass and opposite electric charge. For example, the antiparticle of the electron is the positively charged antielectron, or positron, which is produced naturally in certain types of radioactive decay.The...
carries energy in the other direction; negative and positive on-shell E then simply represent opposing flows of positive energy.

