Orbital inclination change
Encyclopedia
Orbital inclination change is an orbital maneuver
aimed at changing the inclination
of an orbiting body's orbit
. This maneuver is also known as an orbital plane change as the plane of the orbit is tipped. This maneuver requires a change in the orbital velocity vector (delta v) at the orbital nodes (i.e. the point where the initial and desired orbits intersect, the line of orbital nodes is defined by the intersection of the two orbital planes).
Maximum efficiency of inclination change is achieved at apoapsis, (or apogee), where orbital velocity
is the lowest. In some cases, it may require less total delta v to raise the satellite into a higher orbit, change the orbit plane at the higher apogee, and then lower the satellite to its original altitude.
For the most efficient example mentioned above, targeting an inclination at apoapsis also changes the argument of periapsis
. However, targeting in this manner limits the mission designer to changing the plane only along the line of apsides
.
is defined by the angle between ecliptic
North and the vector normal to the orbit plane, (i.e. the angular momentum
vector). This means that inclination is always positive and is entangled with other orbital elements
primarily the argument of periapsis
which is in turn connected to the longitude of the ascending node
. This can result in two very different orbits with precisely the same inclination.
(
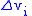) required for an inclination change (
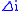) can be calculated as follows: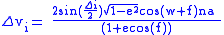
where:
For more complicated manoeuvres which may involve a combination of change in inclination and orbital radius, the amount of delta v is the vector difference between the velocity vectors of the initial orbit and the desired orbit at the transfer point.
= 0) and have the same radius the Delta-v
(
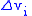) required for an inclination change (
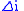) can be calculated using:
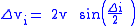
Where:
Transits of other bodies such as the moon can also be done.
Orbital maneuver
In spaceflight, an orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft.For spacecraft far from Earth—for example those in orbits around the Sun—an orbital maneuver is called a deep-space maneuver .-delta-v:...
aimed at changing the inclination
Inclination
Inclination in general is the angle between a reference plane and another plane or axis of direction.-Orbits:The inclination is one of the six orbital parameters describing the shape and orientation of a celestial orbit...
of an orbiting body's orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
. This maneuver is also known as an orbital plane change as the plane of the orbit is tipped. This maneuver requires a change in the orbital velocity vector (delta v) at the orbital nodes (i.e. the point where the initial and desired orbits intersect, the line of orbital nodes is defined by the intersection of the two orbital planes).
Efficiency
In general, inclination changes require the most delta v to perform, and most mission planners try to avoid them whenever possible to conserve fuel. This is typically achieved by launching a spacecraft directly into the desired inclination, or as close to it as possible so as to minimize any inclination change required over the duration of the spacecraft life.Maximum efficiency of inclination change is achieved at apoapsis, (or apogee), where orbital velocity
is the lowest. In some cases, it may require less total delta v to raise the satellite into a higher orbit, change the orbit plane at the higher apogee, and then lower the satellite to its original altitude.For the most efficient example mentioned above, targeting an inclination at apoapsis also changes the argument of periapsis
Argument of periapsis
The argument of periapsis , symbolized as ω, is one of the orbital elements of an orbiting body...
. However, targeting in this manner limits the mission designer to changing the plane only along the line of apsides
Apse line
In astrodynamics, apse line is an imaginary line defined by an orbit's eccentricity vector. It is strictly defined for elliptic, parabolic, and hyperbolic orbits...
.
Inclination entangled with other orbital elements
An important subtlety of performing an inclination change is that Keplerian orbital inclinationInclination
Inclination in general is the angle between a reference plane and another plane or axis of direction.-Orbits:The inclination is one of the six orbital parameters describing the shape and orientation of a celestial orbit...
is defined by the angle between ecliptic
Ecliptic
The ecliptic is the plane of the earth's orbit around the sun. In more accurate terms, it is the intersection of the celestial sphere with the ecliptic plane, which is the geometric plane containing the mean orbit of the Earth around the Sun...
North and the vector normal to the orbit plane, (i.e. the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
vector). This means that inclination is always positive and is entangled with other orbital elements
Orbital elements
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are generally considered in classical two-body systems, where a Kepler orbit is used...
primarily the argument of periapsis
Argument of periapsis
The argument of periapsis , symbolized as ω, is one of the orbital elements of an orbiting body...
which is in turn connected to the longitude of the ascending node
Longitude of the ascending node
The longitude of the ascending node is one of the orbital elements used to specify the orbit of an object in space. It is the angle from a reference direction, called the origin of longitude, to the direction of the ascending node, measured in a reference plane...
. This can result in two very different orbits with precisely the same inclination.
Calculation
In a pure inclination change, only the inclination of the orbit is changed while all other orbital characteristics (radius, shape, etc.) remains the same as before. Delta-vDelta-v
In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....
(
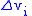) required for an inclination change (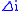) can be calculated as follows: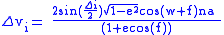where:
is the orbital eccentricityOrbital eccentricityThe orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
is the argument of periapsisArgument of periapsisThe argument of periapsis , symbolized as ω, is one of the orbital elements of an orbiting body...
is the true anomalyTrue anomalyIn celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
is the mean motionMean motionMean motion, n\,\!, is a measure of how fast a satellite progresses around its elliptical orbit. Unless the orbit is circular, the mean motion is only an average value, and does not represent the instantaneous angular rate....
is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
For more complicated manoeuvres which may involve a combination of change in inclination and orbital radius, the amount of delta v is the vector difference between the velocity vectors of the initial orbit and the desired orbit at the transfer point.
Circular orbit inclination change
Where both orbits are circular (i.e. = 0) and have the same radius the Delta-vDelta-v
In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....
(
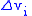) required for an inclination change (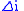) can be calculated using: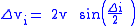Where:
is the orbital velocityOrbital velocityOrbital velocity can refer to the following:* The orbital speed of a body in a gravitational field.* The velocity of particles due to wave motion, in particular in wind waves....
and has the same units as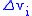
Other ways to change inclination
Some other ways that inclination have been proposed:- aerodynamic lift (for bodies with an atmosphere, such as the Earth)
- tethers
- solar sails
Transits of other bodies such as the moon can also be done.