
Orbital integral
Encyclopedia
In mathematics
, an orbital integral is an integral transform that generalizes the spherical mean
operator to homogeneous space
s. Instead of integrating
over sphere
s, one integrates over generalized spheres: for a homogeneous space X = G/H, a generalized sphere centered at a point x0 is an orbit of the isotropy group of x0.
G/K, where G is a Lie group
and K is a symmetric compact
subgroup
. Generalized spheres are then actual geodesic
spheres and the spherical averaging operator is defined as
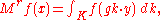
where
Orbital integrals of suitable functions can also be defined on homogeneous spaces G/K where the subgroup K is no longer assumed to be compact, but instead is assumed to be only unimodular. Lorentzian symmetric spaces are of this kind. The orbital integrals in this case are also obtained by integrating over a K-orbit in G/K with respect to the Haar measure of K. Thus
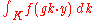
is the orbital integral centered at x over the orbit through y. As above, g is a group element that represents the coset x.
is to reconstruct a function from knowledge of its orbital integrals. The Funk transform
and Radon transform
are two special cases. When G/K is a Riemannian symmetric space, the problem is trivial, since Mrƒ(x) is the average value of ƒ over the generalized sphere of radius r, and

When K is compact (but not necessarily symmetric), a similar trick works. The problem is more interesting when K is non-compact. The Radon transform, for example, is the orbital integral that results by taking G to be the Euclidean isometry group and K the isotropy group of a hyperplane.
Orbital integrals are an important technical tool in the theory of automorphic forms, where they enter into the formulation of various trace formula
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an orbital integral is an integral transform that generalizes the spherical mean
Spherical mean
In mathematics, the spherical mean of a function around a point is the average of all values of that function on a sphere of given radius centered at that point.-Definition:...
operator to homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
s. Instead of integrating
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s, one integrates over generalized spheres: for a homogeneous space X = G/H, a generalized sphere centered at a point x0 is an orbit of the isotropy group of x0.
Definition
The model case for orbital integrals is a Riemannian symmetric spaceRiemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
G/K, where G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and K is a symmetric compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
. Generalized spheres are then actual geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
spheres and the spherical averaging operator is defined as
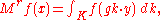
where
- the dot denotes the action of the group G on the homogeneous space X
- g ∈ G is a group element such that x = g·o
- y ∈ X is an arbitrary element of the geodesic sphere of radius r centered at x: d(x,y) = r
- the integration is taken with respect to the Haar measureHaar measureIn mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
on K (since K is compact, it is unimodular and the left and right Haar measures coincide and can be normalized so that the mass of K is 1).
Orbital integrals of suitable functions can also be defined on homogeneous spaces G/K where the subgroup K is no longer assumed to be compact, but instead is assumed to be only unimodular. Lorentzian symmetric spaces are of this kind. The orbital integrals in this case are also obtained by integrating over a K-orbit in G/K with respect to the Haar measure of K. Thus
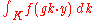
is the orbital integral centered at x over the orbit through y. As above, g is a group element that represents the coset x.
Integral geometry
A central problem of integral geometryIntegral geometry
In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant transformations from the space of functions on one geometrical space to the...
is to reconstruct a function from knowledge of its orbital integrals. The Funk transform
Funk transform
In the mathematical field of integral geometry, the Funk transform is an integral transform defined by integrating a function on great circles of the sphere. It was introduced by Paul Funk in 1916, based on the work of . It is closely related to the Radon transform...
and Radon transform
Radon transform
thumb|right|Radon transform of the [[indicator function]] of two squares shown in the image below. Lighter regions indicate larger function values. Black indicates zero.thumb|right|Original function is equal to one on the white region and zero on the dark region....
are two special cases. When G/K is a Riemannian symmetric space, the problem is trivial, since Mrƒ(x) is the average value of ƒ over the generalized sphere of radius r, and

When K is compact (but not necessarily symmetric), a similar trick works. The problem is more interesting when K is non-compact. The Radon transform, for example, is the orbital integral that results by taking G to be the Euclidean isometry group and K the isotropy group of a hyperplane.
Orbital integrals are an important technical tool in the theory of automorphic forms, where they enter into the formulation of various trace formula
Trace formula
*Arthur–Selberg trace formula*Invariant trace formula*Jacquet's relative trace formula*Kuznetsov trace formula*Local trace formula*Petersson trace formula*Selberg trace formula*Simple trace formula*Stable trace formula...
s.

