
Ostrowski–Hadamard gap theorem
Encyclopedia
In mathematics
, the Ostrowski–Hadamard gap theorem is a result about the analytic continuation
of complex
power series whose non-zero terms are of orders that have a suitable "gap" between them. Such a power series is "badly behaved" in the sense that it cannot be extended to be an analytic function
anywhere on the boundary
of its disc of convergence
. The result is named after the mathematician
s Alexander Ostrowski
and Jacques Hadamard
.
of integer
s such that, for some λ > 1 and all j ∈ N,

Let (αj)j∈N be a sequence of complex numbers such that the power series
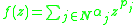
has radius of convergence 1. Then no point z with |z| = 1 is a regular point for f, i.e. f cannot be analytically extended from the open unit disc D to any larger open set including even a single point of the boundary of D.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Ostrowski–Hadamard gap theorem is a result about the analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
power series whose non-zero terms are of orders that have a suitable "gap" between them. Such a power series is "badly behaved" in the sense that it cannot be extended to be an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
anywhere on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of its disc of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
. The result is named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s Alexander Ostrowski
Alexander Ostrowski
Alexander Markowich Ostrowski , was a mathematician.His father Mark having been a merchant, Alexander Ostrowski attended the Kiev College of Commerce, not a high school, and thus had an insufficient qualification to be admitted to university...
and Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
.
Statement of the theorem
Let 0 < p1 < p2 < ... be a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s such that, for some λ > 1 and all j ∈ N,

Let (αj)j∈N be a sequence of complex numbers such that the power series
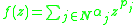
has radius of convergence 1. Then no point z with |z| = 1 is a regular point for f, i.e. f cannot be analytically extended from the open unit disc D to any larger open set including even a single point of the boundary of D.

