
P-Laplacian
Encyclopedia
In mathematics
, the p-Laplacian, or the p-Laplace operator, is a quasilinear elliptic
partial differential operator of 2nd order. It is a generalization of the Laplace operator
, where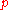 is allowed to range over
is allowed to range over  . It is written as
. It is written as
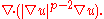
In the special case when , it is the regular Laplacian.
, it is the regular Laplacian.
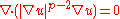
in a domain is the minimizer of the energy functional
is the minimizer of the energy functional

among all functions in the Sobolev space
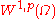 satisfying the boundary conditions in the trace
satisfying the boundary conditions in the trace
sense.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the p-Laplacian, or the p-Laplace operator, is a quasilinear elliptic
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
partial differential operator of 2nd order. It is a generalization of the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, where
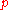 is allowed to range over
is allowed to range over  . It is written as
. It is written as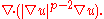
In the special case when
 , it is the regular Laplacian.
, it is the regular Laplacian. Energy formulation
The solution of the p-Laplace equation with Dirichlet boundary conditions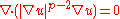
in a domain
 is the minimizer of the energy functional
is the minimizer of the energy functionalEnergy functional
Energy functional is total energy of a certain system, as a function of the system's state.In the energy methods of simulating the dynamics of complex structures, a state of the system is often described as an element of an appropriate function space. To be in this state, the system pays a certain...

among all functions in the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
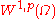 satisfying the boundary conditions in the trace
satisfying the boundary conditions in the traceTrace operator
In mathematics, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problems, that is, to partial differential equations with prescribed boundary conditions...
sense.

