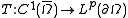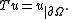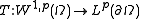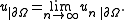Trace operator
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s, that is, to partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s with prescribed boundary conditions. The trace operator makes it possible to extend the notion of restriction of a function to the boundary of its domain to "generalized" functions in a Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
.
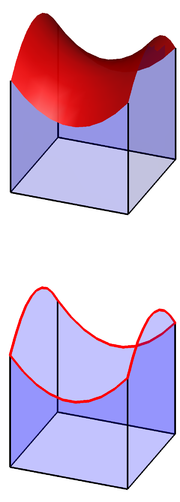
Informal discussion
Let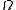 be a bounded
be a boundedBounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
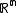 with C1
with C1Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
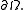 If
If  is a function that is
is a function that is 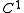 (or even just continuous
(or even just continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
) on the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
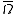 of
of 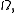 its function restriction is well-defined and continuous on
its function restriction is well-defined and continuous on 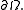 If however,
If however,  is the solution to some partial differential equation, it is in general a weak solution
is the solution to some partial differential equation, it is in general a weak solutionWeak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
, so it belongs to some Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
. Such functions are defined only up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a set of measure zero, and since the boundary
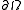 does have measure zero, any function in a Sobolev space can be completely redefined on the boundary without changing the function as an element in that space. It follows that simple function restriction cannot be used to meaningfully define what it means for a general solution to a partial differential equation to behave in a prescribed way on the boundary of
does have measure zero, any function in a Sobolev space can be completely redefined on the boundary without changing the function as an element in that space. It follows that simple function restriction cannot be used to meaningfully define what it means for a general solution to a partial differential equation to behave in a prescribed way on the boundary of 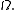
The way out of this difficulty is the observation that while an element
 in a Sobolev space may be ill-defined as a function,
in a Sobolev space may be ill-defined as a function,  can be nevertheless approximated by a sequence
can be nevertheless approximated by a sequence 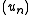 of
of 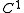 functions defined on the closure of
functions defined on the closure of  Then, the restriction
Then, the restriction  of
of  to
to 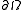 is defined as the limit of the sequence of restrictions
is defined as the limit of the sequence of restrictions  .
.Construction of the trace operator
To rigorously define the notion of restriction to a function in a Sobolev space, let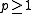 be a real number
be a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. Consider the linear operator
defined on the set of all
 functions on the closure of
functions on the closure of  with values in the Lp space
with values in the Lp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
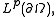 given by the formula
given by the formulaThe domain of
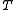 is a subset of the Sobolev space
is a subset of the Sobolev space 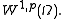 It can be proved that there exists a constant
It can be proved that there exists a constant 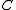 depending only on
depending only on  and
and 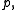 such that
such that-
 for all
for all  in
in 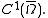
Then, since the
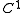 functions on
functions on 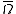 are dense
are denseDense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in
 , the operator
, the operator 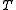 admits a continuous extension
admits a continuous extensiondefined on the entire space
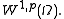
 is called the trace operator. The restriction (or trace)
is called the trace operator. The restriction (or trace) 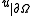 of a function
of a function  in
in 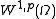 is then defined as
is then defined as 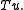
This argument can be made more concrete as follows. Given a function
 in
in 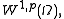 consider a sequence of functions
consider a sequence of functions 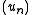 that are
that are 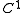 on
on 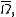 with
with 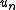 converging to
converging to  in the norm of
in the norm of 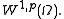 Then, by the above inequality, the sequence
Then, by the above inequality, the sequence 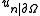 will be convergent in
will be convergent in 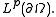 Define
DefineIt can be shown that this definition is independent of the sequence
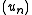 approximating
approximating 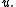
Application
Consider the problem of solving Poisson's equationPoisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
with zero boundary conditions:
-
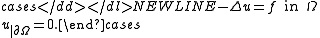
Here,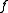 is a given continuous function on
is a given continuous function on 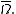
With the help of the concept of trace, define the subspace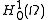 to be all functions in the Sobolev space
to be all functions in the Sobolev space 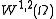 (this space is also denoted
(this space is also denoted 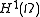 ) whose trace is zero. Then, the equation above can be given the weak formulationWeak formulationWeak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
) whose trace is zero. Then, the equation above can be given the weak formulationWeak formulationWeak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
- Find
 in
in 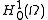 such that
such that -
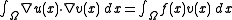 for all
for all  in
in 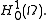
Using the Lax–Milgram theorem one can then prove that this equation has precisely one solution, which implies that the original equation has precisely one weak solution.
One can employ similar ideas to prove the existence and uniqueness of more complicated partial differential equations and with other boundary conditions (such as NeumannNeumann boundary conditionIn mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
and RobinRobin boundary conditionIn mathematics, the Robin boundary condition is a type of boundary condition, named after Victor Gustave Robin . When imposed on an ordinary or a partial differential equation, it is a specification of a linear combination of the values of a function and the values of its derivative on the...
), with the notion of trace playing an important role in all such problems. - Find