
P-chart
Encyclopedia
{mn}
| meanlimits =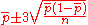
| meanstatistic =
}}
In statistical quality control
, the p-chart is a type of control chart
used to monitor the proportion of nonconforming units
in a sample
, where the sample proportion nonconforming is defined as the ratio of the number of nonconforming units to the sample size, n.
The p-chart only accommodates "pass"/"fail"-type inspection as determined by one or more go-no go gauges
or tests, effectively applying the specifications
to the data before they are plotted on the chart. Other types of control charts display the magnitude of the quality characteristic under study, making troubleshooting possible directly from those charts.
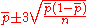 where
where  is the estimate of the long-term process mean established during control-chart setup. Naturally, if the lower control limit is less than or equal to zero, process observations only need be plotted against the upper control limit. Note that observations of proportion nonconforming below a positive lower control limit are cause for concern as they are more frequently evidence of improperly calibrated test and inspection equipment or inadequately trained inspectors than of sustained quality improvement.
is the estimate of the long-term process mean established during control-chart setup. Naturally, if the lower control limit is less than or equal to zero, process observations only need be plotted against the upper control limit. Note that observations of proportion nonconforming below a positive lower control limit are cause for concern as they are more frequently evidence of improperly calibrated test and inspection equipment or inadequately trained inspectors than of sustained quality improvement.
Some organizations may elect to provide a standard value for p, effectively making it a target value for the proportion nonconforming. This may be useful when simple process adjustments can consistently move the process mean, but in general, this makes it more challenging to judge whether a process is fully out of control or merely off-target (but otherwise in control).
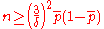 . Another technique is to choose the sample size large enough so that the p-chart has a positive lower control limit or
. Another technique is to choose the sample size large enough so that the p-chart has a positive lower control limit or 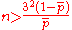 .
.
| meanlimits =
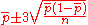
| meanstatistic =

}}
In statistical quality control
Statistical process control
Statistical process control is the application of statistical methods to the monitoring and control of a process to ensure that it operates at its full potential to produce conforming product. Under SPC, a process behaves predictably to produce as much conforming product as possible with the least...
, the p-chart is a type of control chart
Control chart
Control charts, also known as Shewhart charts or process-behaviour charts, in statistical process control are tools used to determine whether or not a manufacturing or business process is in a state of statistical control.- Overview :...
used to monitor the proportion of nonconforming units
Nonconformity (quality)
In quality management, a nonconformity is a deviation from a specification, a standard, or an expectation. Nonconformities are classified as either critical, major, or minor....
in a sample
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
, where the sample proportion nonconforming is defined as the ratio of the number of nonconforming units to the sample size, n.
The p-chart only accommodates "pass"/"fail"-type inspection as determined by one or more go-no go gauges
Go-NoGo gauge
A Go-NoGo gauge refers to an inspection tool used to check a workpiece against its allowed tolerances. Its name derives from its use: the gauge has two tests; the check involves the workpiece having to pass one test and fail the other .It is an integral part of the quality process that is used...
or tests, effectively applying the specifications
Specification (technical standard)
A specification is an explicit set of requirements to be satisfied by a material, product, or service. Should a material, product or service fail to meet one or more of the applicable specifications, it may be referred to as being out of specification;the abbreviation OOS may also be used...
to the data before they are plotted on the chart. Other types of control charts display the magnitude of the quality characteristic under study, making troubleshooting possible directly from those charts.
Assumptions
The binomial distribution is the basis for the p-chart and requires the following assumptions:- The probability of nonconformity is the same for each unit;
- Each unit is independent of its predecessors or successors;
- The inspection procedure is same for each sample and is carried out consistently from sample to sample
Calculation and plotting
The control limits for this chart type are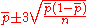 where
where  is the estimate of the long-term process mean established during control-chart setup. Naturally, if the lower control limit is less than or equal to zero, process observations only need be plotted against the upper control limit. Note that observations of proportion nonconforming below a positive lower control limit are cause for concern as they are more frequently evidence of improperly calibrated test and inspection equipment or inadequately trained inspectors than of sustained quality improvement.
is the estimate of the long-term process mean established during control-chart setup. Naturally, if the lower control limit is less than or equal to zero, process observations only need be plotted against the upper control limit. Note that observations of proportion nonconforming below a positive lower control limit are cause for concern as they are more frequently evidence of improperly calibrated test and inspection equipment or inadequately trained inspectors than of sustained quality improvement.Some organizations may elect to provide a standard value for p, effectively making it a target value for the proportion nonconforming. This may be useful when simple process adjustments can consistently move the process mean, but in general, this makes it more challenging to judge whether a process is fully out of control or merely off-target (but otherwise in control).
Potential pitfalls
There are two circumstances that merit special attention:- Ensuring enough observations are taken for each sample
- Accounting for differences in the number of observations from sample to sample
Adequate sample size
Sampling requires some careful consideration. If the organization elects to use 100% inspection on a process, the production rate determines an appropriate sampling rate which in turn determines the sample size. If the organization elects to only inspect a fraction of units produced, the sample size should be chosen large enough so that the chance of finding at least one nonconforming unit in a sample is high—otherwise the false alarm rate is too high. One technique is to fix sample size so that there is a 50% chance of detecting a process shift of a given amount (for example, from 1% defective to 5% defective). If δ is the size of the shift to detect, then the sample size should be set to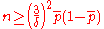 . Another technique is to choose the sample size large enough so that the p-chart has a positive lower control limit or
. Another technique is to choose the sample size large enough so that the p-chart has a positive lower control limit or 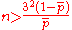 .
.Varying sample sizes
In the case of 100% inspection, variation in the production rate (e.g., due to maintenance or shift changes) conspires to produce different sample sizes for each observation plotted on the p-chart. There are three ways to deal with this:| Technique | Description |
|---|---|
| Use variable-width control limits | Each observation plots against its own control limits:  , where ni is the size of the sample that produced the ith observation on the p-chart , where ni is the size of the sample that produced the ith observation on the p-chart |
| Use control limits based on an average sample size | Control limits are  , where , where  is the average size of all the samples on the p-chart, is the average size of all the samples on the p-chart, 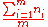 |
| Use a standardized control chart | Control limits are ±3 and the observations, 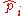 , are standardized , are standardizedStandard score In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation... using 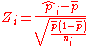 , where ni is the size of the sample that produced the ith observation on the p-chart , where ni is the size of the sample that produced the ith observation on the p-chart |

