
Padé table
Encyclopedia
In complex analysis
, a Padé table is an array, possibly of infinite extent, of the rational Padé approximant
s
to a given complex formal power series
. Certain sequences of approximants lying within a Padé table can often be shown to correspond with successive convergents
of a continued fraction
representation of a holomorphic or meromorphic function.
s, Frobenius
(in 1881) was apparently the first to organize the approximants in the form of a table. Henri Padé
further expanded this notion in his doctoral thesis Sur la representation approchee d'une fonction par des fractions rationelles, in 1892. Over the ensuing 16 years Padé published 28 additional papers exploring the properties of his table, and relating the table to analytic continued fractions.
Modern interest in Padé tables was revived by H. S. Wall
and Oskar Perron
, who were primarily interested in the connections between the tables and certain classes of continued fractions. Daniel Shanks
and Peter Wynn
published influential papers about 1955, and W. B. Gragg obtained far-reaching convergence results during the '70s. More recently, the widespread use of electronic computers has stimulated a great deal of additional interest in the subject.
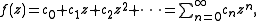
where c0 ≠ 0, by convention. The (m, n)th entry Rm, n in the Padé table for f(z) is then given by
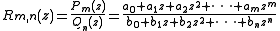
where Pm(z) and Qn(z) are polynomials of degrees not more than m and n, respectively. The coefficients {ai} and {bi} can always be found by considering the expression
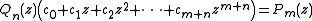
and equating coefficients of like powers of z up through m + n. For the coefficients of powers m + 1 to m + n, the right hand side is 0 and the resulting system of linear equations contains a homogeneous system of n equations in the n + 1 unknowns bi, and so admits of infinitely many solutions each of which determines a possible Qn. Pm is then easily found by equating the first m coefficients of the equation above. However, it can be shown that, due to cancellation, the generated rational functions Rm, n are all the same, so that the (m, n)th entry in the Padé table is unique. Alternatively, we may require that b0 = 1, thus putting the table in a standard form.
Although the entries in the Padé table can always be generated by solving this system of equations, that approach is computationally expensive. More efficient methods have been devised, including the epsilon algorithm.
is a power series whose first term is of degree no less than
If the first term of that difference is of degree
then the rational function Rm, n occupies
2
cells in the Padé table, from position (m, n) through position (m+r, n+r), inclusive. In other words, if the same rational function appears more than once in the table, that rational function occupies a square block of cells within the table. This result is known as the block theorem.
If a particular rational function occurs exactly once in the Padé table, it is called a normal approximant to f(z). If every entry in the complete Padé table is normal, the table itself is said to be normal. Normal Padé approximants can be characterized using determinant
s of the coefficients cn in the Taylor series expansion of f(z), as follows. Define the (m, n)th determinant by
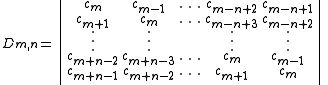
with Dm,0 = 1, Dm,1 = cm, and ck = 0 for k < 0. Then
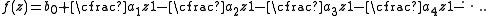
where the ai ≠ 0 are complex constants, and z is a complex variable.
There is an intimate connection between regular C-fractions and Padé tables with normal approximants along the main diagonal: the "stairstep" sequence of Padé approximants R0,0, R1,0, R1,1, R2,1, R2,2, … is normal if and only if that sequence coincides with the successive convergents
of a regular C-fraction. In other words, if the Padé table is normal along the main diagonal, it can be used to construct a regular C-fraction, and if a regular C-fraction representation for the function f(z) exists, then the main diagonal of the Padé table representing f(z) is normal.
.
Several interesting features are immediately apparent.
The procedure used to derive Gauss's continued fraction can be applied to a certain confluent hypergeometric series to derive the following C-fraction expansion for the exponential function, valid throughout the entire complex plane:
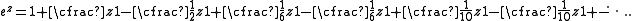
By applying the fundamental recurrence formulas
one may easily verify that the successive convergents of this C-fraction are the stairstep sequence of Padé approximants R0,0, R1,0, R1,1, … Interestingly, in this particular case a closely related continued fraction can be obtained from the identity
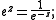
that continued fraction looks like this:

This fraction's successive convergents also appear in the Padé table, and form the sequence R0,0, R0,1, R1,1, R1,2, R2,2, …
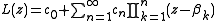
where the sequence {βk} of points in the complex plane is known as the set of interpolation points. A sequence of rational approximants Rm,n can be formed for such a series L in a manner entirely analogous to the procedure described above, and the approximants can be arranged in a Newton-Padé table. It has been shown that some "staircase" sequences in the Newton-Padé table correspond with the successive convergents of a Thiele-type continued fraction, which is of the form
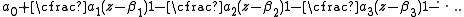
Mathematicians have also constructed two-point Padé tables by considering two series, one in powers of z, the other in powers of 1/z, which alternately represent the function f(z) in a neighborhood of zero and in a neighborhood of infinity.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a Padé table is an array, possibly of infinite extent, of the rational Padé approximant
Padé approximant
Padé approximant is the "best" approximation of a function by a rational function of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating....
s
- Rm, n
to a given complex formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
. Certain sequences of approximants lying within a Padé table can often be shown to correspond with successive convergents
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
of a continued fraction
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
representation of a holomorphic or meromorphic function.
History
Although earlier mathematicians had obtained sporadic results involving sequences of rational approximations to transcendental functionTranscendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
s, Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
(in 1881) was apparently the first to organize the approximants in the form of a table. Henri Padé
Henri Padé
Henri Eugène Padé was a French mathematician, who is now remembered mainly for his development of approximation techniques for functions using rational functions.He was educated at École Normale Supérieure in Paris...
further expanded this notion in his doctoral thesis Sur la representation approchee d'une fonction par des fractions rationelles, in 1892. Over the ensuing 16 years Padé published 28 additional papers exploring the properties of his table, and relating the table to analytic continued fractions.
Modern interest in Padé tables was revived by H. S. Wall
Hubert Stanley Wall
Hubert Stanley Wall was an American mathematician who worked primarily in the field of continued fractions. He is also known as one of the leading proponents of the Moore method of teaching....
and Oskar Perron
Oskar Perron
Oskar Perron was a German mathematician.He was a professor at the University of Heidelberg from 1914 to 1922 and at the University of Munich from 1922 to 1951...
, who were primarily interested in the connections between the tables and certain classes of continued fractions. Daniel Shanks
Daniel Shanks
Daniel Shanks was an American mathematician who worked primarily in numerical analysis and number theory. He is best known as the first to compute π to 100,000 decimal places, and for his book Solved and Unsolved Problems in Number Theory.-Life and education:Dan Shanks was born on January 17,...
and Peter Wynn
Peter Wynn (mathematician)
Peter Wynn is a mathematician. His main achievements concern approximation theory – in particular the theory of Padé approximants – and its application in numerical methods for improving the rate of convergence of sequences of real numbers....
published influential papers about 1955, and W. B. Gragg obtained far-reaching convergence results during the '70s. More recently, the widespread use of electronic computers has stimulated a great deal of additional interest in the subject.
Notation
A function f(z) is represented by a formal power series: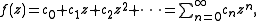
where c0 ≠ 0, by convention. The (m, n)th entry Rm, n in the Padé table for f(z) is then given by
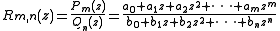
where Pm(z) and Qn(z) are polynomials of degrees not more than m and n, respectively. The coefficients {ai} and {bi} can always be found by considering the expression
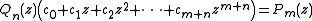
and equating coefficients of like powers of z up through m + n. For the coefficients of powers m + 1 to m + n, the right hand side is 0 and the resulting system of linear equations contains a homogeneous system of n equations in the n + 1 unknowns bi, and so admits of infinitely many solutions each of which determines a possible Qn. Pm is then easily found by equating the first m coefficients of the equation above. However, it can be shown that, due to cancellation, the generated rational functions Rm, n are all the same, so that the (m, n)th entry in the Padé table is unique. Alternatively, we may require that b0 = 1, thus putting the table in a standard form.
Although the entries in the Padé table can always be generated by solving this system of equations, that approach is computationally expensive. More efficient methods have been devised, including the epsilon algorithm.
The block theorem and normal approximants
Because of the way the (m, n)th approximant is constructed, the difference- Qn(z)f(z) − Pm(z)
is a power series whose first term is of degree no less than
- m + n + 1.
If the first term of that difference is of degree
- m + n + r + 1, r > 0,
then the rational function Rm, n occupies
2
cells in the Padé table, from position (m, n) through position (m+r, n+r), inclusive. In other words, if the same rational function appears more than once in the table, that rational function occupies a square block of cells within the table. This result is known as the block theorem.
If a particular rational function occurs exactly once in the Padé table, it is called a normal approximant to f(z). If every entry in the complete Padé table is normal, the table itself is said to be normal. Normal Padé approximants can be characterized using determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s of the coefficients cn in the Taylor series expansion of f(z), as follows. Define the (m, n)th determinant by
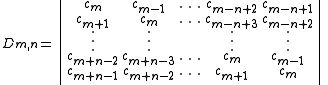
with Dm,0 = 1, Dm,1 = cm, and ck = 0 for k < 0. Then
- the (m, n)th approximant to f(z) is normal if and only if none of the four determinants Dm,n−1, Dm,n, Dm+1,n, and Dm+1,n+1 vanish; and
- the Padé table is normal if and only if none of the determinants Dm,n are equal to zero (note in particular that this means none of the coefficients ck in the series representation of f(z) can be zero).
Connection with continued fractions
One of the most important forms in which an analytic continued fraction can appear is as a regular C-fraction, which is a continued fraction of the form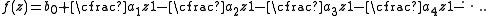
where the ai ≠ 0 are complex constants, and z is a complex variable.
There is an intimate connection between regular C-fractions and Padé tables with normal approximants along the main diagonal: the "stairstep" sequence of Padé approximants R0,0, R1,0, R1,1, R2,1, R2,2, … is normal if and only if that sequence coincides with the successive convergents
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
of a regular C-fraction. In other words, if the Padé table is normal along the main diagonal, it can be used to construct a regular C-fraction, and if a regular C-fraction representation for the function f(z) exists, then the main diagonal of the Padé table representing f(z) is normal.
An example – the exponential function
Here is an example of a Padé table, for the exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
.
| m \ n | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 |  |
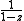 |
 |
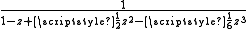 |
| 1 | 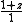 |
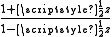 |
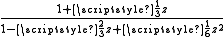 |
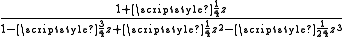 |
| 2 | 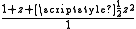 |
 |
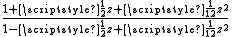 |
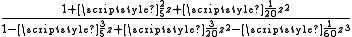 |
| 3 | 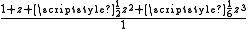 |
 |
 |
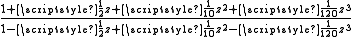 |
| 4 | 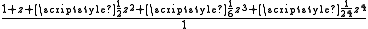 |
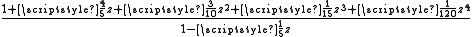 |
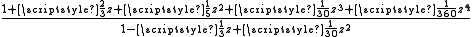 |
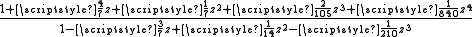 |
Several interesting features are immediately apparent.
- The first column of the table consists of the successive truncations of the Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for ez. - Similarly, the first row contains the reciprocals of successive truncations of the series expansion of e−z.
- The approximants Rm,n and Rn,m are quite symmetrical – the numerators and denominators are interchanged, and the patterns of plus and minus signs are different, but the same coefficients appear in both of these approximants. In fact, using the
 notation of generalized hypergeometric series,
notation of generalized hypergeometric series,
-

- Computations involving the Rn,n (on the main diagonal) can be done quite efficiently. For example, R3,3 reproduces the power series for the exponential function perfectly up through 1/720 z6, but because of the symmetry of the two cubic polynomials, a very fast evaluation algorithm can be devised.
The procedure used to derive Gauss's continued fraction can be applied to a certain confluent hypergeometric series to derive the following C-fraction expansion for the exponential function, valid throughout the entire complex plane:
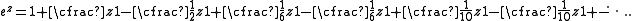
By applying the fundamental recurrence formulas
Fundamental recurrence formulas
In the theory of continued fractions, the fundamental recurrence formulas relate the partial numerators and the partial denominators with the numerators and denominators of the fraction's successive convergents...
one may easily verify that the successive convergents of this C-fraction are the stairstep sequence of Padé approximants R0,0, R1,0, R1,1, … Interestingly, in this particular case a closely related continued fraction can be obtained from the identity
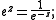
that continued fraction looks like this:

This fraction's successive convergents also appear in the Padé table, and form the sequence R0,0, R0,1, R1,1, R1,2, R2,2, …
Generalizations
A formal Newton series L is of the form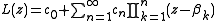
where the sequence {βk} of points in the complex plane is known as the set of interpolation points. A sequence of rational approximants Rm,n can be formed for such a series L in a manner entirely analogous to the procedure described above, and the approximants can be arranged in a Newton-Padé table. It has been shown that some "staircase" sequences in the Newton-Padé table correspond with the successive convergents of a Thiele-type continued fraction, which is of the form
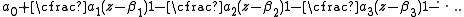
Mathematicians have also constructed two-point Padé tables by considering two series, one in powers of z, the other in powers of 1/z, which alternately represent the function f(z) in a neighborhood of zero and in a neighborhood of infinity.

