Pairwise summation
Encyclopedia
In numerical analysis
, pairwise summation, also called cascade summation, is a technique to sum a sequence of finite-precision floating-point numbers that substantially reduces the accumulated round-off error
compared to naively accumulating the sum in sequence. Although there are other techniques such as Kahan summation that typically have even smaller round-off errors, pairwise summation is nearly as good (differing only by a logarithmic factor) while having much lower computational cost—it can be implemented so as to have nearly the same cost (and exactly the same number of arithmetic operations) as naive summation.
In particular, pairwise summation of a sequence of n numbers xn works by recursively
breaking the sequence into two halves, summing each half, and adding the two sums: a divide and conquer algorithm
. Its roundoff errors grow asymptotically
as at most O(ε log n), where ε is the machine precision (assuming a fixed condition number
, as discussed below). In comparison, the naive technique of accumulating the sum in sequence (adding each xi one at a time for i = 1, ..., n) has roundoff errors that grow at worst as O(εn). Kahan summation has a worst-case error of roughly O(ε), independent of n, but requires several times more arithmetic operations. If the roundoff errors are random, and in particular have random signs, then they form a random walk
and the error growth is reduced to an average of
for pairwise summation.
Precisely the recursive structure of pairwise summation is found in many fast Fourier transform
(FFT) algorithms, and is responsible for the same slow roundoff accumulation of those FFTs.
, the pairwise summation algorithm for an array
x of length n can be written:
s = pairwise(x[1…n])
if n ≤ N base case: naive summation for a sufficiently small array
s = x[1]
for i = 2 to n
s = s + x[i]
else divide and conquer: recursively sum two halves of the array
m = floor(n / 2)
s = pairwise(x[1…m]) + pairwise(x[m+1…n])
endif
For some sufficiently small N, this algorithm switches to a naive loop-based summation as a base case, whose error bound is O(εN). Therefore, the entire sum has a worst-case error that grows asymptotically as O(εN log n) for large n, for a given condition number (see below), and the smallest error bound is attained for N = 1.
In an algorithm of this sort (as for divide and conquer algorithms in general), it is desirable to use a larger base case in order to amortize
the overhead of the recursion. If N = 1, then there is roughly one recursive subroutine call for every input, but more generally there is one recursive call for (roughly) every N/2 inputs if the recursion stops at exactly n = N. By making N sufficiently large, the overhead of recursion can be made negligible (precisely this technique of a large base case for recursive summation is employed by high-performance FFT implementations).
Regardless of N, exactly n−1 additions are performed in total, the same as for naive summation, so if the recursion overhead is made negligible then pairwise summation has essentially the same computational cost as for naive summation.
A variation on this idea is to break the sum into b blocks at each recursive stage, summing each block recursively, and then summing the results, which was dubbed a "superblock" algorithm by its proposers. The above pairwise algorithm corresponds to b = 2 for every stage except for the last stage which is b = N.
(computed with infinite precision).
With pairwise summation for a base case N = 1, one instead obtains
, where the error 
is bounded above by:
where ε is the machine precision of the arithmetic being employed (e.g. ε ≈ 10−16 for standard double precision
floating point). Usually, the quantity of interest is the relative error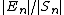
, which is therefore bounded above by:
In the expression for the relative error bound, the fraction (Σ|xi|/|Σxi|) is the condition number
of the summation problem. Essentially, the condition number represents the intrinsic sensitivity of the summation problem to errors, regardless of how it is computed. The relative error bound of every (backwards stable) summation method by a fixed algorithm in fixed precision (i.e. not those that use arbitrary precision arithmetic, nor algorithms whose memory and time requirements change based on the data), is proportional to this condition number. An ill-conditioned summation problem is one in which this ratio is large, and in this case even pairwise summation can have a large relative error. For example, if the summands xi are uncorrelated random numbers with zero mean, the sum is a random walk
and the condition number will grow proportional to
. On the other hand, for random inputs with nonzero mean the condition number asymptotes to a finite constant as 
. If the inputs are all non-negative, then the condition number is 1.
Note that the
denominator is effectively 1 in practice, since 
is much smaller than 1 until n becomes of order 21/ε, which is roughly 101015 in double precision.
In comparison, the relative error bound for naive summation (simply adding the numbers in sequence, rounding at each step) grows as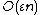
multiplied by the condition number. In practice, it is much more likely that the rounding errors have a random sign, with zero mean, so that they form a random walk; in this case, naive summation has a root mean square
relative error that grows as
and pairwise summation as an error that grows as 
on average.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, pairwise summation, also called cascade summation, is a technique to sum a sequence of finite-precision floating-point numbers that substantially reduces the accumulated round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
compared to naively accumulating the sum in sequence. Although there are other techniques such as Kahan summation that typically have even smaller round-off errors, pairwise summation is nearly as good (differing only by a logarithmic factor) while having much lower computational cost—it can be implemented so as to have nearly the same cost (and exactly the same number of arithmetic operations) as naive summation.
In particular, pairwise summation of a sequence of n numbers xn works by recursively
Recursion (computer science)
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
breaking the sequence into two halves, summing each half, and adding the two sums: a divide and conquer algorithm
Divide and conquer algorithm
In computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
. Its roundoff errors grow asymptotically
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
as at most O(ε log n), where ε is the machine precision (assuming a fixed condition number
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
, as discussed below). In comparison, the naive technique of accumulating the sum in sequence (adding each xi one at a time for i = 1, ..., n) has roundoff errors that grow at worst as O(εn). Kahan summation has a worst-case error of roughly O(ε), independent of n, but requires several times more arithmetic operations. If the roundoff errors are random, and in particular have random signs, then they form a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
and the error growth is reduced to an average of
for pairwise summation.Precisely the recursive structure of pairwise summation is found in many fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) algorithms, and is responsible for the same slow roundoff accumulation of those FFTs.
The algorithm
In pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
, the pairwise summation algorithm for an array
Array data type
In computer science, an array type is a data type that is meant to describe a collection of elements , each selected by one or more indices that can be computed at run time by the program. Such a collection is usually called an array variable, array value, or simply array...
x of length n can be written:
s = pairwise(x[1…n])
if n ≤ N base case: naive summation for a sufficiently small array
s = x[1]
for i = 2 to n
s = s + x[i]
else divide and conquer: recursively sum two halves of the array
m = floor(n / 2)
s = pairwise(x[1…m]) + pairwise(x[m+1…n])
endif
For some sufficiently small N, this algorithm switches to a naive loop-based summation as a base case, whose error bound is O(εN). Therefore, the entire sum has a worst-case error that grows asymptotically as O(εN log n) for large n, for a given condition number (see below), and the smallest error bound is attained for N = 1.
In an algorithm of this sort (as for divide and conquer algorithms in general), it is desirable to use a larger base case in order to amortize
Amortized analysis
In computer science, amortized analysis is a method of analyzing algorithms that considers the entire sequence of operations of the program. It allows for the establishment of a worst-case bound for the performance of an algorithm irrespective of the inputs by looking at all of the operations...
the overhead of the recursion. If N = 1, then there is roughly one recursive subroutine call for every input, but more generally there is one recursive call for (roughly) every N/2 inputs if the recursion stops at exactly n = N. By making N sufficiently large, the overhead of recursion can be made negligible (precisely this technique of a large base case for recursive summation is employed by high-performance FFT implementations).
Regardless of N, exactly n−1 additions are performed in total, the same as for naive summation, so if the recursion overhead is made negligible then pairwise summation has essentially the same computational cost as for naive summation.
A variation on this idea is to break the sum into b blocks at each recursive stage, summing each block recursively, and then summing the results, which was dubbed a "superblock" algorithm by its proposers. The above pairwise algorithm corresponds to b = 2 for every stage except for the last stage which is b = N.
Accuracy
Suppose that one is summing n values xi, for i = 1, ..., n. The exact sum is:(computed with infinite precision).
With pairwise summation for a base case N = 1, one instead obtains
, where the error is bounded above by:where ε is the machine precision of the arithmetic being employed (e.g. ε ≈ 10−16 for standard double precision
Double precision
In computing, double precision is a computer number format that occupies two adjacent storage locations in computer memory. A double-precision number, sometimes simply called a double, may be defined to be an integer, fixed point, or floating point .Modern computers with 32-bit storage locations...
floating point). Usually, the quantity of interest is the relative error
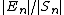, which is therefore bounded above by:In the expression for the relative error bound, the fraction (Σ|xi|/|Σxi|) is the condition number
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
of the summation problem. Essentially, the condition number represents the intrinsic sensitivity of the summation problem to errors, regardless of how it is computed. The relative error bound of every (backwards stable) summation method by a fixed algorithm in fixed precision (i.e. not those that use arbitrary precision arithmetic, nor algorithms whose memory and time requirements change based on the data), is proportional to this condition number. An ill-conditioned summation problem is one in which this ratio is large, and in this case even pairwise summation can have a large relative error. For example, if the summands xi are uncorrelated random numbers with zero mean, the sum is a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
and the condition number will grow proportional to
. On the other hand, for random inputs with nonzero mean the condition number asymptotes to a finite constant as . If the inputs are all non-negative, then the condition number is 1.Note that the
denominator is effectively 1 in practice, since is much smaller than 1 until n becomes of order 21/ε, which is roughly 101015 in double precision.In comparison, the relative error bound for naive summation (simply adding the numbers in sequence, rounding at each step) grows as
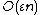multiplied by the condition number. In practice, it is much more likely that the rounding errors have a random sign, with zero mean, so that they form a random walk; in this case, naive summation has a root mean squareRoot mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
relative error that grows as
and pairwise summation as an error that grows as on average.