Parabolic Lie algebra
Encyclopedia
In algebra
, a parabolic Lie algebra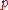
is a subalgebra of a semisimple Lie algebra 
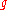satisfying one of the following two conditions:
These conditions are equivalent over an algebraically closed field
of characteristic zero, such as the complex numbers. If the field
is not algebraically closed, then the first condition is replaced by the assumption that
where
is the algebraic closure
of
.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, a parabolic Lie algebra
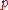is a subalgebra of a semisimple Lie algebra 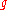satisfying one of the following two conditions:
-
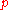contains a maximal solvable subalgebra (a Borel subalgebra) of 
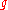; - the Killing perpKilling formIn mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
of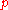
in 
is the nilradical of 
.
These conditions are equivalent over an algebraically closed field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic zero, such as the complex numbers. If the field
is not algebraically closed, then the first condition is replaced by the assumption that
-
contains a Borel subalgebra of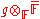 
where
is the algebraic closureAlgebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of
.