Parallel axis theorem
Encyclopedia
In physics
, the parallel axis theorem or Huygens-Steiner
theorem can be used to determine the second moment of area
or the mass moment of inertia of a rigid body
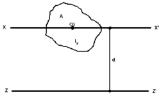
about any axis, given the body's moment of inertia about a parallel
axis through the object's centre of mass and the perpendicular
distance
(r) between the axes.
The moment of inertia about the new axis z is given by:
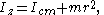
where:
is the moment of inertia of the object about an axis passing through its centre of mass;
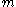is the object's mass;
is the perpendicular distance between the two axes.
This rule can be applied with the stretch rule
and perpendicular axis theorem
to find moments of inertia for a variety of shapes.
The parallel axes rule also applies to the second moment of area
(area moment of inertia)
for a plane region D:
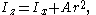
where:
is the area moment of inertia of D relative to the parallel axis;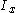
is the area moment of inertia of D relative to its centroid
;
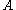is the area of the plane region D;
is the distance from the new axis z to the centroid
of the plane region D.
Note: The centroid
of D coincides with the centre of gravity (CG) of a physical plate
with the same shape that has uniform density.
the perpendicular distance between the axes lies along the x-axis and that the centre of mass lies at the origin. The moment of inertia relative to the z-axis, passing through the centre of mass, is:
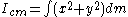
The moment of inertia relative to the new axis, perpendicular distance r along the x-axis from the centre of mass, is:
If we expand the brackets, we get:
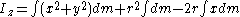
The first term is Icm, the second term becomes mr2, and the final term is zero since the origin is at the centre of mass. So, this expression becomes:
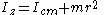
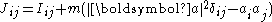
where
is the displacement vector from the centre of mass to the new axis, and
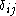
is the Kronecker delta.
We can see that, for diagonal elements (when i = j), displacements perpendicular to the axis of rotation results in the above simplified version of the parallel axis theorem.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the parallel axis theorem or Huygens-Steiner
Jakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
theorem can be used to determine the second moment of area
Second moment of area
The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...
or the mass moment of inertia of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
about any axis, given the body's moment of inertia about a parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
axis through the object's centre of mass and the perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
(r) between the axes.
The moment of inertia about the new axis z is given by:
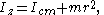
where:
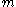is the moment of inertia of the object about an axis passing through its centre of mass; is the object's mass; is the perpendicular distance between the two axes.This rule can be applied with the stretch rule
Stretch rule
In physics, the stretch rule states that the moment of inertia of a rigid object is unchanged when the object is stretched parallel to the axis of rotation,...
and perpendicular axis theorem
Perpendicular axis theorem
In physics, the perpendicular axis theorem can be used to determine the moment of inertia of a rigid object that lies entirely within a plane, about an axis perpendicular to the plane, given the moments of inertia of the object about two perpendicular axes lying within the plane...
to find moments of inertia for a variety of shapes.
The parallel axes rule also applies to the second moment of area
Second moment of area
The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...
(area moment of inertia)
for a plane region D:
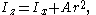
where:
is the area moment of inertia of D relative to the parallel axis;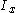 is the area moment of inertia of D relative to its centroidCentroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
;
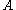is the area of the plane region D; is the distance from the new axis z to the centroidCentroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
of the plane region D.
Note: The centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
of D coincides with the centre of gravity (CG) of a physical plate
with the same shape that has uniform density.
Proof
We may assume, without loss of generality, that in a Cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
the perpendicular distance between the axes lies along the x-axis and that the centre of mass lies at the origin. The moment of inertia relative to the z-axis, passing through the centre of mass, is:
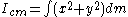
The moment of inertia relative to the new axis, perpendicular distance r along the x-axis from the centre of mass, is:
If we expand the brackets, we get:
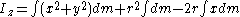
The first term is Icm, the second term becomes mr2, and the final term is zero since the origin is at the centre of mass. So, this expression becomes:
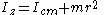
In classical mechanics
In classical mechanics, the Parallel axis theorem (also known as Huygens-Steiner theorem) can be generalized to calculate a new inertia tensor Jij from an inertia tensor about a centre of mass Iij when the pivot point is a displacement a from the centre of mass: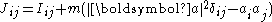where
is the displacement vector from the centre of mass to the new axis, and
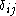
is the Kronecker delta.
We can see that, for diagonal elements (when i = j), displacements perpendicular to the axis of rotation results in the above simplified version of the parallel axis theorem.
See also
- Perpendicular axis theoremPerpendicular axis theoremIn physics, the perpendicular axis theorem can be used to determine the moment of inertia of a rigid object that lies entirely within a plane, about an axis perpendicular to the plane, given the moments of inertia of the object about two perpendicular axes lying within the plane...
- Stretch ruleStretch ruleIn physics, the stretch rule states that the moment of inertia of a rigid object is unchanged when the object is stretched parallel to the axis of rotation,...
- Jakob SteinerJakob SteinerJakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
- Christiaan Huygens