
Paranormal subgroup
Encyclopedia
In mathematics
, in the field of group theory
, a paranormal subgroup is a subgroup
such that the subgroup generated
by it and any conjugate
of it, is also generated by it and a conjugate of it within that subgroup.
In symbols,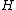 is paranormal in
is paranormal in 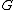 if given any
if given any  in
in 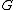 , the subgroup
, the subgroup 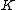 generated by
generated by 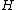 and
and 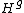 is also equal to
is also equal to 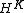 . Equivalently, a subgroup is paranormal if its weak closure and normal closure coincide in all intermediate subgroups.
. Equivalently, a subgroup is paranormal if its weak closure and normal closure coincide in all intermediate subgroups.
Here are some facts relating paranormality to other subgroup properties:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a paranormal subgroup is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
such that the subgroup generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by it and any conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
of it, is also generated by it and a conjugate of it within that subgroup.
In symbols,
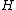 is paranormal in
is paranormal in 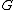 if given any
if given any  in
in 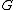 , the subgroup
, the subgroup 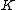 generated by
generated by 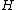 and
and 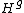 is also equal to
is also equal to 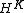 . Equivalently, a subgroup is paranormal if its weak closure and normal closure coincide in all intermediate subgroups.
. Equivalently, a subgroup is paranormal if its weak closure and normal closure coincide in all intermediate subgroups.Here are some facts relating paranormality to other subgroup properties:
- Every pronormal subgroupPronormal subgroupIn mathematics, especially in the field of group theory, a pronormal subgroup is a subgroup that is embedded in a nice way. Pronormality is a simultaneous generalization of both normal subgroups and abnormal subgroups such as Sylow subgroups, ....
, and hence, every normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
and every abnormal subgroupAbnormal subgroupIn mathematics, in the field of group theory, an abnormal subgroup is a subgroup H of a group G such that for every x ∈ G, x lies in the subgroup generated by H and H x....
, is paranormal. - Every paranormal subgroup is a polynormal subgroupPolynormal subgroupIn mathematics, in the field of group theory, a subgroup of a group is said to be polynormal if its closure under conjugation by any element of the group can also be achieved via closure by conjugation by some element in the subgroup generated....
. - In finite solvable groups, every polynormal subgroup is paranormal.

