
Parity function
Encyclopedia
In Boolean algebra, a parity function is a Boolean function whose value is 1 if the input vector has an odd number of ones.
The parity function is notable for its role in theoretical investigation of circuit complexity
of Boolean functions.
 -variable parity function is the Boolean function
-variable parity function is the Boolean function 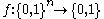 with the property that
with the property that 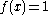 if and only if
if and only if
the number of ones in the vector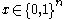 is odd.
is odd.
In other words,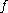 is defined as follows:
is defined as follows: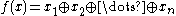 .
.
.
The n-variable parity function and its negation are the only Boolean functions for which all disjunctive normal form
s have the maximal number of 2 n − 1 monomial
s of length n and all conjunctive normal form
s have the maximal number of 2 n − 1 clauses of length n.
and independently Miklós Ajtai
established super-polynomial lower bounds on the size of constant-depth Boolean circuits for the parity function, i.e., they showed that polynomial-size constant-depth circuits cannot compute the parity function. Similar results were also established for the majority, multiplication and transitive closure functions, by reduction from the parity function.
established tight exponential lower bounds on the size of constant-depth Boolean circuits for the parity function. Håstad's Switching Lemma is the key technical tool used for these lower bounds and Johan Håstad
was awarded the Gödel Prize
for this work in 1994.
The precise result is that depth-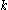 circuits with AND, OR, and NOT gates require size
circuits with AND, OR, and NOT gates require size 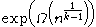 to compute the parity function.
to compute the parity function.
This is asymptotically almost optimal as there are depth-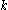 circuits computing parity which have size
circuits computing parity which have size 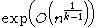 .
.
 mapping every infinite binary string to 0 or 1, having the following property: if
mapping every infinite binary string to 0 or 1, having the following property: if 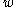 and
and  are infinite binary strings differing only on finite number of coordinates then
are infinite binary strings differing only on finite number of coordinates then 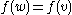 if and only if
if and only if 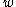 and
and  differ on even number of coordinates.
differ on even number of coordinates.
Assuming axiom of choice it can be easily proved that parity functions exist and there are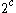 many of them - as many as the number of all functions from
many of them - as many as the number of all functions from 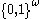 to
to 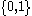 . It is enough to take one representative per equivalence class of relation
. It is enough to take one representative per equivalence class of relation 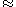 defined as follows:
defined as follows: 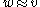 iff
iff 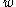 and
and  differ at finite number of coordinates. Having such representatives, we can map all of them to 0; the rest of
differ at finite number of coordinates. Having such representatives, we can map all of them to 0; the rest of 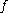 values are deducted unambiguously.
values are deducted unambiguously.
Infinite parity functions are often used in theoretical Computer Science and Set Theory because of their simple definition and - on the other hand - their descriptive complexity. For example, it can be shown that an inverse image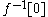 is a non-Borel set.
is a non-Borel set.
The parity function is notable for its role in theoretical investigation of circuit complexity
Circuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of Boolean circuits that compute them....
of Boolean functions.
Definition
The -variable parity function is the Boolean function
-variable parity function is the Boolean function 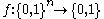 with the property that
with the property that 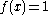 if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the number of ones in the vector
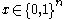 is odd.
is odd.In other words,
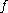 is defined as follows:
is defined as follows: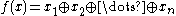 .
.Properties
Parity only depends on the number of ones and is therefore a symmetric Boolean functionSymmetric Boolean function
In mathematics, a symmetric Boolean function is a Boolean function whose value does not depend on the permutation of its input bits, i.e., it depends only on the number of ones in the input....
.
The n-variable parity function and its negation are the only Boolean functions for which all disjunctive normal form
Disjunctive normal form
In boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
s have the maximal number of 2 n − 1 monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s of length n and all conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
s have the maximal number of 2 n − 1 clauses of length n.
Circuit complexity
In the early 1980s, Merrick Furst, James Saxe and Michael SipserMichael Sipser
Michael Fredric Sipser is a professor of Applied Mathematics in the Theory of Computation Group at the Massachusetts Institute of Technology. He received his Ph.D. in 1980 from the University of California, Berkeley under the direction of Manuel Blum....
and independently Miklós Ajtai
Miklós Ajtai
Miklós Ajtai is a computer scientist at the IBM Almaden Research Center. In 2003 he received the Knuth Prize for his numerous contributions to the field, including a classic sorting network algorithm Miklós Ajtai (born 2 July 1946, Budapest, Hungary) is a computer scientist at the IBM Almaden...
established super-polynomial lower bounds on the size of constant-depth Boolean circuits for the parity function, i.e., they showed that polynomial-size constant-depth circuits cannot compute the parity function. Similar results were also established for the majority, multiplication and transitive closure functions, by reduction from the parity function.
established tight exponential lower bounds on the size of constant-depth Boolean circuits for the parity function. Håstad's Switching Lemma is the key technical tool used for these lower bounds and Johan Håstad
Johan Håstad
Johan Torkel Håstad is a Swedish theoretical computer scientist most known for his work on computational complexity theory. He was the recipient of the Gödel Prize in 1994 and 2011 and the ACM Doctoral Dissertation Award in 1986, among other prizes...
was awarded the Gödel Prize
Gödel Prize
The Gödel Prize is a prize for outstanding papers in theoretical computer science, named after Kurt Gödel and awarded jointly by the European Association for Theoretical Computer Science and the Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory .The...
for this work in 1994.
The precise result is that depth-
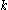 circuits with AND, OR, and NOT gates require size
circuits with AND, OR, and NOT gates require size 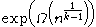 to compute the parity function.
to compute the parity function.This is asymptotically almost optimal as there are depth-
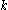 circuits computing parity which have size
circuits computing parity which have size 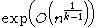 .
.Infinite version
An infinite parity function is a function mapping every infinite binary string to 0 or 1, having the following property: if
mapping every infinite binary string to 0 or 1, having the following property: if 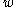 and
and  are infinite binary strings differing only on finite number of coordinates then
are infinite binary strings differing only on finite number of coordinates then 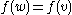 if and only if
if and only if 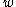 and
and  differ on even number of coordinates.
differ on even number of coordinates.Assuming axiom of choice it can be easily proved that parity functions exist and there are
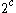 many of them - as many as the number of all functions from
many of them - as many as the number of all functions from 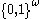 to
to 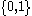 . It is enough to take one representative per equivalence class of relation
. It is enough to take one representative per equivalence class of relation 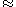 defined as follows:
defined as follows: 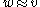 iff
iff 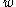 and
and  differ at finite number of coordinates. Having such representatives, we can map all of them to 0; the rest of
differ at finite number of coordinates. Having such representatives, we can map all of them to 0; the rest of 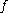 values are deducted unambiguously.
values are deducted unambiguously.Infinite parity functions are often used in theoretical Computer Science and Set Theory because of their simple definition and - on the other hand - their descriptive complexity. For example, it can be shown that an inverse image
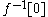 is a non-Borel set.
is a non-Borel set.

