Parity game
Encyclopedia
A parity game is played on a colored directed graph
, where each node has been colored by a priority – one of (usually) finitely many natural numbers. Two players, 0 and 1, take turns moving a token along the edges of the graph, resulting in a (possibly infinite) path
, called the play.
The winner of a finite play is the player whose opponent is unable to move. The winner of an infinite play is determined by the priorities appearing in the play. Typically, player 0 wins an infinite play if the smallest priority that occurs infinitely often in the play is even. Player 1 wins otherwise. This explains the word "parity" in the title.
Parity games lie in the third level of the borel hierarchy
, and are consequently determined
.
Games related to parity games were implicitly used in Rabin
's
proof of decidability of second order theory of n successors, where determinacy
of such games was
proven. The Knaster–Tarski theorem leads to a relatively simple proof of determinacy of parity games.
Moreover, parity games are history-free determined. This means that if a player has a winning strategy then she has a winning strategy that depends only on the current board position, and not on the history of the play.
and Co-NP, as well as UP
and co-UP.Grädel 2007, p. 163 It remains an open question whether this decision problem is solvable in PTime
.
Given that parity games are history-free determined, solving a given parity game is equivalent to solving the following simple looking graph-theoretic problem. Given a finite colored directed bipartite graph
with n vertices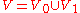
, and V colored with colors from 1 to m, is there a choice function selecting a single out-going edge from each vertex of 
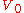, such that the resulting subgraph has the property that in each cycle the smallest occurring color is even.
. The modified game has the Rabin acceptance condition.
Specifically, in the above bipartite graph scenario, the problem now is to determine if there
is a choice function selecting a single out-going edge from each vertex of V0, such that the resulting subgraph has the property that in each cycle (and hence each strongly connected component
) it is the case that there exists an i and a node with color 2i, and no node with color 2i − 1..
Note that as opposed to parity games, this game is no longer symmetric with respect to players 0 and 1.
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
, where each node has been colored by a priority – one of (usually) finitely many natural numbers. Two players, 0 and 1, take turns moving a token along the edges of the graph, resulting in a (possibly infinite) path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
, called the play.
The winner of a finite play is the player whose opponent is unable to move. The winner of an infinite play is determined by the priorities appearing in the play. Typically, player 0 wins an infinite play if the smallest priority that occurs infinitely often in the play is even. Player 1 wins otherwise. This explains the word "parity" in the title.
Parity games lie in the third level of the borel hierarchy
Borel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
, and are consequently determined
Determinacy
In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
.
Games related to parity games were implicitly used in Rabin
Michael O. Rabin
Michael Oser Rabin , is an Israeli computer scientist and a recipient of the Turing Award.- Biography :Rabin was born in 1931 in Breslau, Germany, , the son of a rabbi. In 1935, he emigrated with his family to Mandate Palestine...
's
proof of decidability of second order theory of n successors, where determinacy
Determinacy
In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
of such games was
proven. The Knaster–Tarski theorem leads to a relatively simple proof of determinacy of parity games.
Moreover, parity games are history-free determined. This means that if a player has a winning strategy then she has a winning strategy that depends only on the current board position, and not on the history of the play.
Solving a game
Solving a parity game played on a finite graph means deciding, for a given starting position, which of the two players has a winning strategy. It has been shown that this problem is in NPNP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
and Co-NP, as well as UP
UP (complexity)
In complexity theory, UP is the complexity class of decision problems solvable in polynomial time on a non-deterministic Turing machine with at most one accepting path for each input...
and co-UP.Grädel 2007, p. 163 It remains an open question whether this decision problem is solvable in PTime
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
.
Given that parity games are history-free determined, solving a given parity game is equivalent to solving the following simple looking graph-theoretic problem. Given a finite colored directed bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
with n vertices
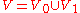, and V colored with colors from 1 to m, is there a choice function selecting a single out-going edge from each vertex of 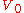, such that the resulting subgraph has the property that in each cycle the smallest occurring color is even.Related games and their decision problems
A slight modification of the above game, and the related graph-theoretic problem, makes solving the game NP-hardNP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
. The modified game has the Rabin acceptance condition.
Specifically, in the above bipartite graph scenario, the problem now is to determine if there
is a choice function selecting a single out-going edge from each vertex of V0, such that the resulting subgraph has the property that in each cycle (and hence each strongly connected component
Strongly connected component
A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....
) it is the case that there exists an i and a node with color 2i, and no node with color 2i − 1..
Note that as opposed to parity games, this game is no longer symmetric with respect to players 0 and 1.
Further reading
- E. Grädel, W. Thomas, T. Wilke (Eds.) : Automata, Logics, and Infinite Games, Springer LNCS 2500 (2003), ISBN 3540003886