The Peaucellier–Lipkin linkage (or Peaucellier–Lipkin cell, or Peaucellier–Lipkin Inversor), invented in 1864, was the first planar linkage

Linkage (mechanical)

A mechanical linkage is an assembly of bodies connected together to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for...

 capable of transforming rotary motion into perfect straight-line motion, and vice versa. It is named after Charles-Nicolas Peaucellier

Charles-Nicolas Peaucellier

Charles-Nicolas Peaucellier was a French engineer who graduated from the École polytechnique. He made a career in the French army and was promoted to général de division in 1888....

 (1832–1913), a French army officer, and Yom Tov Lipman Lipkin, a Lithuanian Jew and son of the famed Rabbi Israel Salanter.

Until this invention, no planar method existed of producing straight motion without reference guideways, making the linkage especially important as a machine component and for manufacturing. In particular, a piston

Piston

A piston is a component of reciprocating engines, reciprocating pumps, gas compressors and pneumatic cylinders, among other similar mechanisms. It is the moving component that is contained by a cylinder and is made gas-tight by piston rings. In an engine, its purpose is to transfer force from...

 head needs to keep a good seal with the shaft in order to retain the driving (or driven) medium. The Peaucellier linkage was important in the development of the steam engine

Steam engine

A steam engine is a heat engine that performs mechanical work using steam as its working fluid.Steam engines are external combustion engines, where the working fluid is separate from the combustion products. Non-combustion heat sources such as solar power, nuclear power or geothermal energy may be...

.

The mathematics of the Peaucellier–Lipkin linkage is directly related to the inversion of a circle.

There is an earlier straight-line mechanism, whose history is not well known, called Sarrus linkage

Sarrus linkage

The Sarrus linkage, invented in 1853 by Pierre Frédéric Sarrus, is a mechanical linkage to convert a limited circular motion to a linear motion without reference guideways. The linkage uses two perpendicular hinged rectangular plates positioned parallel over each other...

. This linkage predates the Peaucellier–Lipkin linkage by 11 years and consists of a series of hinged rectangular plates, two of which remain parallel but can be moved normally to each other. Sarrus' linkage is of a three-dimensional class sometimes known as a space crank, unlike the Peaucellier–Lipkin linkage which is a planar mechanism.

Geometry

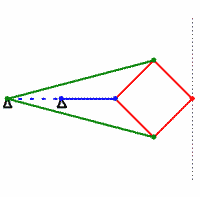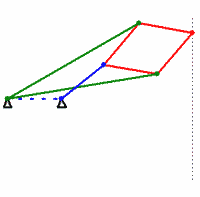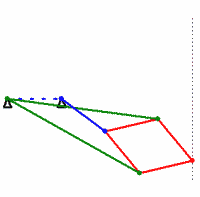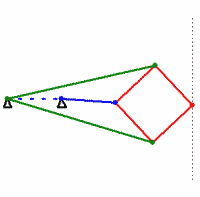
In the geometric diagram of the apparatus, six bars of fixed length can be seen: OA, OC, AB, BC, CD, DA. The length of OA is equal to the length of OC, and the lengths of AB, BC, CD, and DA are all equal forming a rhombus

Rhombus

In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...

. Also, point O is fixed. Then, if point B is constrained to move along a circle (shown in red) which passes through O, then point D will necessarily have to move along a straight line (shown in blue). On the other hand, if point B were constrained to move along a line (not passing through O), then point D would necessarily have to move along a circle (passing through O).

Collinearity

First, it must be proven that points O, B, D are collinear

Line (geometry)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

.

Triangles BAD and BCD are congruent because side BD is congruent to itself, side BA is congruent to side BC, and side AD is congruent to side CD. Therefore angles ABD and CBD are equal.

Next, triangles OBA and OBC are congruent, since sides OA and OC are congruent, side OB is congruent to itself, and sides BA and BC are congruent. Therefore angles OBA and OBC are equal.

Angle OBA + angle ABD + angle DBC + angle CBO = 360°
but angle OBA = angle OBC and angle DBA = angle DBC, thus

2 × angle OBA + 2 × angle DBA = 360°

angle OBA + angle DBA = 180°

therefore points O, B, and D are collinear.

Inverse points

Let point P be the intersection of lines AC and BD. Then, since ABCD is a rhombus

Rhombus

In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...

, P is the midpoint

Midpoint

The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...

 of both line segments BD and AC. Therefore length BP = length PD.

Triangle BPA is congruent to triangle DPA, because side BP is congruent to side DP, side AP is congruent to itself, and side AB is congruent to side AD. Therefore angle BPA = angle DPA. But since angle BPA + angle DPA = 180°, then 2 × angle BPA = 180°, angle BPA = 90°, and angle DPA = 90°.

Let:
Then:
(due to the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

) (Pythagorean theorem)
Since OA and AD are both fixed lengths, then the product of OB and OD is a constant:
and since points O, B, D are collinear, then D is the inverse of B with respect to the circle (O,k) with center O and radius k.

Inversive geometry

Thus, by the properties of inversive geometry, since the figure traced by point D is the inverse of the figure traced by point B, if B traces a circle passing through the center of inversion O, then D is constrained to trace a straight line. But if B traces a straight line not passing through O, then D must trace an arc of a circle passing through O. Q.E.D.

Q.E.D.

Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...

Historical notes

Sylvester

James Joseph Sylvester

James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...

 (Collected Works, Vol. 3 Paper2 ) writes that when he showed a model to Kelvin, he 'nursed it as if it had been his own child, and when a motion was made to relieve him of it, replied "No! I have not had nearly enough of it—it is the most beautiful thing I have ever seen in my life"'.

External links

• How to Draw a Straight Line, online video clips of linkages with interactive applets.
• How to Draw a Straight Line, historical discussion of linkage design
• Interactive Java Applet with proof.
• Java animated Peaucellier–Lipkin linkage
• Jewish Encyclopedia article on Lippman Lipkin and his father Israel Salanter
• Peaucellier Apparatus features an interactive applet
• A simulation using the Molecular Workbench software
• A related linkage called Hart's Inversor.