
Pebble Motion Problems
Encyclopedia
The pebble motion problems, or pebble motion on graphs, are a set of related problems in graph theory
dealing with the movement of multiple objects ("pebbles") from vertex to vertex in a graph
with a constraint on the number of pebbles that can occupy a vertex at any time. Pebble motion problems occur in domains such as multi-robot
motion planning
(in which the pebbles are robots) and network routing (in which the pebbles are packets of data). The best-known example of a pebble motion problem is Sam Loyd's
famous 15-puzzle.
Let be a graph with
be a graph with  vertices. Let
vertices. Let 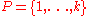 be a set of pebbles with
be a set of pebbles with  . An arrangement of pebbles is a mapping
. An arrangement of pebbles is a mapping  such that
such that 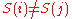 for
for 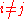 . A move consists
. A move consists 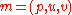 of transferring pebble
of transferring pebble 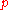 from vertex
from vertex  to adjacent unoccupied vertex
to adjacent unoccupied vertex  . The Pebble Motion on Graphs problem is to decide, given two arrangements
. The Pebble Motion on Graphs problem is to decide, given two arrangements  and
and  , whether there is a sequence of moves that transforms
, whether there is a sequence of moves that transforms  into
into  .
.
Another set of variations consider the case in which some or all of the pebbles are unlabeled and interchangeable.
Other versions of the problem seek not only to prove reachability but to find a (potentially optimal) sequence of moves (i.e. a plan) which performs the transformation.
. The same applies to the unlabeled problem .
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
dealing with the movement of multiple objects ("pebbles") from vertex to vertex in a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
with a constraint on the number of pebbles that can occupy a vertex at any time. Pebble motion problems occur in domains such as multi-robot
Robot
A robot is a mechanical or virtual intelligent agent that can perform tasks automatically or with guidance, typically by remote control. In practice a robot is usually an electro-mechanical machine that is guided by computer and electronic programming. Robots can be autonomous, semi-autonomous or...
motion planning
Motion planning
Motion planning is a term used in robotics for the process of detailing a task into discrete motions....
(in which the pebbles are robots) and network routing (in which the pebbles are packets of data). The best-known example of a pebble motion problem is Sam Loyd's
Sam Loyd
Samuel Loyd , born in Philadelphia and raised in New York, was an American chess player, chess composer, puzzle author, and recreational mathematician....
famous 15-puzzle.
Theoretical formulation
The general form of the pebble motion problem is Pebble Motion on Graphs formulated as follows:Let
 be a graph with
be a graph with  vertices. Let
vertices. Let 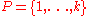 be a set of pebbles with
be a set of pebbles with  . An arrangement of pebbles is a mapping
. An arrangement of pebbles is a mapping  such that
such that 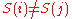 for
for 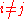 . A move consists
. A move consists 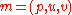 of transferring pebble
of transferring pebble  from vertex
from vertex  to adjacent unoccupied vertex
to adjacent unoccupied vertex  . The Pebble Motion on Graphs problem is to decide, given two arrangements
. The Pebble Motion on Graphs problem is to decide, given two arrangements  and
and  , whether there is a sequence of moves that transforms
, whether there is a sequence of moves that transforms  into
into  .
.Variations
Common variations on the problem limit the structure of the graph to be:- a tree
- a square gridLattice graphThe terms lattice graph, mesh graph, or grid graph refer to a number of categories of graphs whose drawing corresponds to some grid/mesh/lattice, i.e., its vertices correspond to the nodes of the mesh and its edges correspond to the ties between the nodes.-Square grid graph:A common type of a...
, - a bi-connectedBiconnected graphIn the mathematical discipline of graph theory, a biconnected graph is a connected graph with no articulation vertices.In other words, a biconnected graph is connected and nonseparable, meaning that if any vertex were to be removed, the graph will remain connected.The property of being 2-connected...
graph.
Another set of variations consider the case in which some or all of the pebbles are unlabeled and interchangeable.
Other versions of the problem seek not only to prove reachability but to find a (potentially optimal) sequence of moves (i.e. a plan) which performs the transformation.
Complexity
Finding the shortest path in the pebble motion on graphs problem (with labeled pebbles) is known to be NP-hard and APX-hardAPX
In complexity theory the class APX is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant...
. The same applies to the unlabeled problem .

